Tangent lines to circles

The equations of the following tangents to one or two circles are calculated. The constructions are drawn and the construction lines are shown if necessary.

• The tangent to a circle k at a point B.
• The tangents to a circle k through a point P outside the circle
• The tangents to a circle k parallel to a straight line g
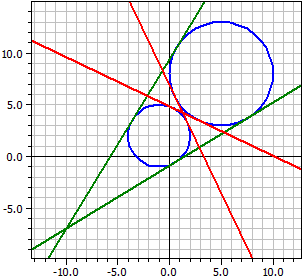
• The tangents to two circles  k₁  and  k₂ 

Example 1:

Given: 
¯¯¯¯¯
  k: M(5|8), r=8.48528, B(-1|2)              

Tangent to k in B 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t: x + y = 1

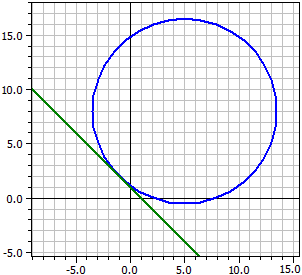
Example 2:

Given:
¯¯¯¯¯
k : M(5|8) ,   r=5 ,    P(-1|2)

Tangents to k through P
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t1: 1,06014·x − 6,77319·y = -14,6065
  t2: 6,77319·x − 1,06014·y = -8,89348

Points of contact
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  k n t1 = B1(5,77319|3,06014)
  k n t2 = B2(0,0601439|8,77319)

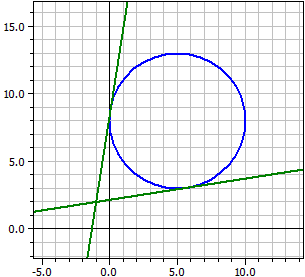
Example 3:

Given:
¯¯¯¯¯
  k : M(5|8) ,   r=5 ,      g : -x + 3·y = 0  

Tangents on k parallel to g
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t1: x − 3·y = -3,18861
  t2: x − 3·y = -34,8114

Points of contact
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  k n t1 = B1(6,58114|3,25658)
  k n t2 = B2(3,41886|12,7434)

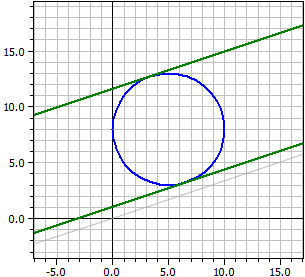
Example 4:

Given:
¯¯¯¯¯
  k1 : M(5|8) ,    r=5
  k2 : M(-1|2) ,   r=3

Outer tangents
¯¯¯¯¯¯¯¯¯¯¯¯
  t1: -4,2923·x + 7,04104·y = -6,36427
  t2: -7,04104·x + 4,29230·y = 40,3643

Inner tangents
¯¯¯¯¯¯¯¯¯¯¯¯
  t3: 1,21895·x + 2,55228·y = 12,3709
  t4: -2,55228·x − 1,21895·y = -8,3709

See also:

Wikipedia: Tangent lines to circles