Sequences and Series
The program determines the first n terms of a sequence (ai) and the associated series (sum of the sequence terms) if the first terms of the sequence and an explicit function ai=ƒ(i) or a recourse formula ai=ƒ(a0, a1, ... , ai-1) are given.
The sequence of odd numbers
It can be defined explicitly by ai = 2·i + 1 :
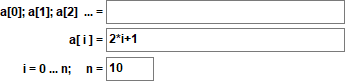
or recursively by ai = ai-1 + 2 with a0=1 .
Sequence ¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Serie ¯¯¯¯ ( Σ a[ i ] ) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
The corresponding series is obviously the sequence of the square numbers. This can be proven very nicely by complete induction.
The Fibonacci sequence
One of the most popular recursive sequences starts with a0=1 and a1=1 . The other terms are equal to the sum of the previous two.
Sequence ¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Serie ¯¯¯¯ ( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
See also:
Wikipedia: Sequence | Fibonacci number