Transformer des polynômes
Un polynôme p(x) peut être déplacé ou étiré dans la direction x et la direction y.
p(x) = a9 x9 + a8 x8 + ... + a0 .
Les coefficients du polynôme peuvent être entrés sous forme de fractions, de nombres mixtes ou de nombres décimaux décomposés.

ƒ(x) = - 1/4 x4 + 2 x3 - 16 x + 21 Déplacé par dx = -2, dy = 0 ƒ(x + 2) = - 1/4 * x4 + 6 * x2 + 1
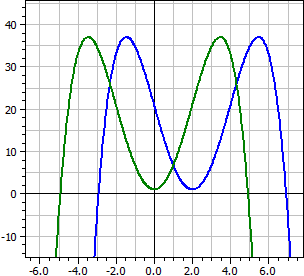
Dans l'exemple, la fonction ƒ(x) a l'axe de symétrie a: x = 2. En décalant 2 pas vers la gauche, nous obtenons la fonction ƒ(x + 2), qui est symétrique à l'axe des y et n'a donc que des exposants avec des puissances paires de x.
Échange de données via le presse-papiers de Windows
Toutes les parties de programme dans lesquelles les coefficients d'un polynôme sont entrés ont un menu contextuel (bouton droit de la souris) avec lequel vous pouvez copier les entrées d'une partie de programme dans le presse-papiers et les coller à partir de là dans une autre partie de programme.
Les coefficients de la fonction transformée sont automatiquement copiés dans le presse-papiers.
De cette façon, les fonctions ƒ(x) et ƒ(x + 2) ont été copiées par copier-coller dans la partie du programme traceur de fonctions . La fonction coller convertit automatiquement la table des coefficients en terme de fonction.
D'autres exemples:
ƒ(x) = x5 + 10·x4 + 36·x3 + 56·x2 + 33·x + 3 Déplacé par dx = 2, dy = 1 ƒ(x -2) + 1 = x5 - 4·x3 + x + 2
ƒ(x) = 1/4·x4 + 2·x2 - 1 Allongé par sx = 2, sy = 1 ƒ(1/2 x) = 1/64·x4 + 1/2·x2 - 1
ƒ(x) = 1/4·x4 + 2·x2 - 1 Allongé par sx = 1/2, sy = 3 3·ƒ(2·x) = 12·x4 + 24·x2 - 3
ƒ(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 Allongé par sx = -1, sy = 9 9·ƒ(-1·x) = - 9·x5 - 81·x4 + 246·x3 + 738·x2

