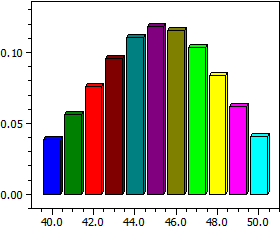
Distribuzione binomiale

Per una variabile casuale X distribuita da b(k;n;p) con n e p indicati, il programma calcola:

• Un istogramma di probabilità P(X=k)
• I loro valori numerici in un intervallo [k_min ; k_max ]
• La probabilità P(k_min ≤ X ≤ k_max )

Teoria:

Da un'urna con una porzione di palline rosse, vengono estratte n palline che vengono immagazzinate all'interno. La variabile casuale X indica quante palle disegnate sono rosse. La probabilità che k delle sfere disegnate siano rosse è contrassegnata con P(X=k) = b(k;n;p).

Inseriamo i valori di n e p, tuttavia p come probabilità deve essere inserito 0 e 1. Successivamente un semplice istogramma fornisce una panoramica dei valori di P (X = k). In una tabella di valori, sono elencati i valori numerici.

Esempio:

  n = 60;    p = .75

     k           P(X=k)          P(0 ≤ X < k)
  ——    ——————   ——————
    40      0,03834033      0,09248427 
    41      0,05610780      0,14859207 
    42      0,07614630      0,22473838 
    43      0,09562559      0,32036397 
    44      0,11083875      0,43120273 
    45      0,11822800      0,54943073 
    46      0,11565783      0,66508856 
    47      0,10335381      0,76844237 
    48      0,08397497      0,85241733 
    49      0,06169589      0,91411323 
    50      0,04071929      0,95483252 
  ——    ——————   ——————
  P(40 ≤ k < 50) =           0,90068858

Vedi anche:

Wikipedia: Distribuzione binomiale