Triangles by three Elements
Triangles are defined by three external properties (sides or angles) if one of the following congruencies is met:
- SSS three sides are given.
- SAA one side and two angles are given.
- SAS two sides and the enclosed angle are given.
- SsA two sides and the angle opposite of the greater side are given.
Given three external properties (sides or angles) of a triangle, the program calculates the sides, the angles, the altitudes, the medians and the angle bisectors, the perimeter and the area, as well as the centers and the radii of the incircle and the circumcircle of the triangle.
In addition the program draws the triangle with its incircle and its circumcircle.
If you enter two sides and the angle opposite of the shorter side, you will get two solutions if they exist.
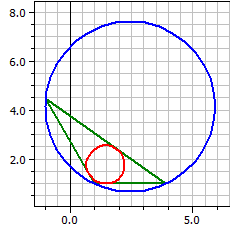
Example 1:
Given: a=6, b=4 and α=60°
Vertices : A(1|1) B(7,899|1) C(3|4,4641)
Sides : 6 4 6,89898
Angles : 60° 35,2644° 84,7356°
Altitudes : 3,98313 5,97469 3,4641
Medians : 4,77472 6,148 3,75513
Bisectr. : 4,38551 6,11664 3,5464
Circumcir.: M(4,44949|1,31784) ru = 3,4641
Incircle : O(3,44949|2,41421) r i = 1,41421
Area : A = 11,9494 Perimeter : u = 16,899
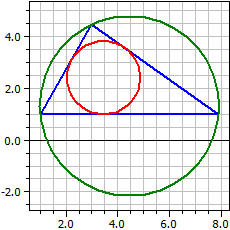
Example 2:
Given: a = 6, b = 4, β = 35,2644
1st Solution:
Vertices : A(1|1) B(7,899|1) C(3|4,464)
Sides : 6 4 6,89898
Angles : 60° 35,2644° 84,7356°
Altitudes : 3,98313 5,97469 3,46410
Medians : 4,77472 6,14800 3,75513
Winkelh.: 4,38550 6,11664 3,5464
Circumcir.: M(4,449|1,3178) ru = 3,4641
Incircle : O(3,449|2,4142) r i = 1,41421
Area : A = 11,9494 Perimeter : u = 16,899
—————————————————————
2nd Solution:
Vertices : A(1|1) B(3,899|1) C(-1|4,464)
Sides : 6 4 2,89898
Angles : 120° 35,2644° 24,7356°
Altitudes : 1,67373 2,51059 3,46410
Medians : 1,78943 4,26639 4,88866
Bisectr. : 1,68082 3,72554 4,68861
Circumcir.: M(2,449|4,146) ru = 3,4641
Incircle : O(1,449|1,779) r i = 0,7785
Area : A = 5,0212 Perimeter : u = 12,899