Plane through three Points
Three non-collinear points define exactly one plane. Given the coordinates of three points the program computes the equation of this plane in the point-slope form and in the form of coordinates as well as its distance from the origin with the directional vectors and the normal vectors being increased to integers. In addition to this the position of the plane in the space is plotted including its lines intersecting a cube symmetric to the axis as well as its trace points.
Example:
Plane through the points:
A(1|2|3), B(2|3|3), C(1|0|1)
Point-slope-form:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
Equation in coordinates:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Distance from origin:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Trace points:
¯¯¯¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0), Sy(0|-2|0), Sz(0|0|2)
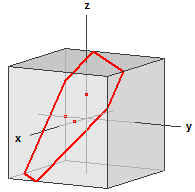
The diagram can be rotated with the left mouse button and be zoomed with the right mouse button.
See also:
Graphics 3DWikipedia: Plane (geometry)

