Hypergeometric Distribution

For a h(k;n;m;r) distributed random variable X with fixed n, m and r you can compute a histogram and a table of values for the probabilities P( X = k ).

This routine is paticularly useful because, due to the four input variables, there are hardly any tables for the hypergeometric distribution and the calculation of probabilities requires a great deal of effort.

Theory:

A container is filled with m balls, r of which are red. If n balls are drawn without replacement, then the random variable X tells, how many red balls have been drawn. The probability that k of the balls drawn are red, is given by P(X=k) = h(k,n,m,r).

The number of balls drawn n, the total number m and the number of red balls r are entered. Since the drawing proceeds without discarding, it is checked that n<m, and also r<m.

Example:

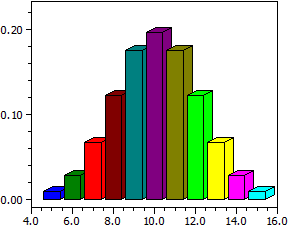
  n = 20;    m = 100;    r = 50

     k         P(X=k)            P(0 ≤ X < k)
  ——   ——————    ——————
     5       0,00889760      0,01141749 
     6       0,02780501      0,03922250 
     7       0,06613084      0,10535334 
     8       0,12160243      0,22695577 
     9       0,17460862      0,40156439 
    10      0,19687122      0,59843561 
    11      0,17460862      0,77304423 
    12      0,12160243      0,89464666 
    13      0,06613084      0,96077750 
    14      0,02780501      0,98858251 
    15      0,00889760      0,99748011 
  ——   ——————    ——————
  P(5 ≤ k < 15) =             0,99496023