Análisis combinatorio

Se calculan las cantidades de posibilidades para seleccionar k de n elementos, estableciendo el valor en secuencia o no (es decir, variación o combinación), y permitiendo repeticiones o no.

Ejemplo:

n = 49
k = 6

Variaciónes sin repetitiones            = 10 068 347 520
Variaciónes con repeticiones          = 13 841 287 201
Combinaciones sin repetitiones      = 13 983 816
Combinaciones con repeticiones    = 25 827 165

Permutaciones de k  :                k ! = 720

Fórmulas:

	Disordenado (combinaciones)	Ordenado (variaciones)	Ordenado y k = n (permutaciones)
Sin repeticiones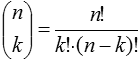
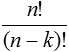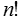Con repeticiones;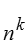

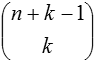En el modelo de urna, la selección con repeticiones corresponde a un sorteo con reemplazo, y la selección sin repeticiones a un sorteo sin reemplazo. La selección ordenada implica que las bolas se extraen una por una, mientras que la selección no ordenada implica que se extraen simultáneamente.

Voir aussi:

Wikipedia: Combinatoria enumerativa