Tangentes a círculos - Cálculo
Polo y Polar
El círculo k alrededor del centro M con
radio r se describe por la ecuación (x - xM)2 + (y - yM)2 = r2 .
Si inserta las coordenadas del punto P en uno de los factores de los cuadrados de la izquierda, obtendrá la siguiente ecuación, que describe una línea recta.
(xP - xM)· (x - xM) + (yP - yM)· (y - yM) = r2 .
Se llama polar al polo P y es una ayuda poderosa en la determinación de las ecuaciones tangentes.
Las tangentes a un círculo k a través de un punto P.
Si se dan un círculo k y un punto P en el círculo, entonces el polar de P es la tangente deseada
Dado un círculo k y un punto P fuera de k, el polar de P intersecta el círculo en los dos puntos de contacto de las tangentes a través de P. así que la ecuación del polar se resuelve para y (o para x si el coeficiente de y es cero) e insertarlo en la ecuación circular. Con los puntos de contacto B1 y B2 calculados de esta manera, se establecen las ecuaciones de las tangentes
Si el punto P se encuentra dentro del círculo, el polar es una línea recta fuera del círculo. Todos los puntos en esto tienen la propiedad de que su polar se cruza en P.
Las tangentes a un círculo k paralelo a una línea recta g
Si se dan un círculo k y una línea recta g: a x + b y = c, entonces la línea perpendicular en g a través del centro M del círculo se cruza con esto en los puntos de contacto B1 y B2 . Para los coeficientes de la recta perpendicular se aplica
Las tangentes a dos círculos k1 y k2
Si r1 y r2 son los radios de los círculos k1 y k2, suponemos s.p.d.g. que r1>r2. Si no, los círculos se intercambian.
La cantidad de tangentes comunes que tienen dos círculos depende de la posición mutua de los círculos:

| M1M2| < r1 − r2

| M1M2| = r1 − r2

r1 − r2 < | M1M2| < r1 + r2
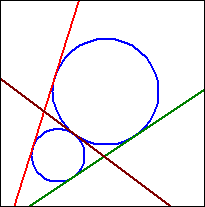
| M1M2| = r1 + r2
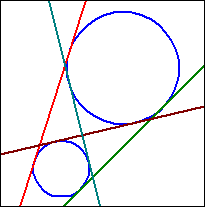
| M1M2| > r1 + r2
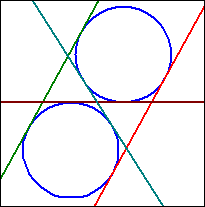
Caso especial r1 = r2
a) | M1M2| = r1 − r2
La forma más fácil de calcular el punto de contacto común B es sumar el r2/| M1M2| veces del vector de M1 a M22 al vector de posición de M2. La tangente es la perpendicular a (M1M2) en B.
b) | M1M2| > r1 − r2
Para determinar las tangentes externas a dos círculos, primero se determinan las tangentes de M2 a un círculo k3 alrededor de M1 con radio r3 = r1 − r2 (análogo a "Tangente a k a través de P"). Si P1 y P2 son los puntos de contacto en k3, puede desplazarlos en r1/ r3 veces el vector de M1 a P1 o P2 resp. para obtener los puntos de contacto B1 y B2 (cf. a)).
Dos círculos con el mismo radio forman un caso especial, ya que el círculo auxiliar k3 tendría un radio de cero. En este caso las tangentes se determinan análogamente a "Tangente a k paralela a g" con g = (M1M2).
c) | M1M2| = r1 + r2
Si los dos círculos se tocan desde el exterior, hay una tercera tangente común t3 . El punto de contacto común divide la distancia M1 M2 en la relación r1:r2. La tangente t3 es ortogonal a M1M2.
d) | M1M2| > r1 + r2
Si k2 está completamente fuera de k1,hay dos tangentes comunes "internas" que se cruzan entre los círculos.
Para determinar las tangentes internas a dos círculos, primero se determinan las tangentes de M2 a un círculo k3 alrededor de M1 con radio r3= r1+ r2 (análogo a "Tangente a k a través de P"). Si P1 y P2 son los puntos de contacto en k3, entonces estos se desplazan por r1/ r3 veces el vector de M1 a P1 o P2 resp. (cf. a)).

