MatheAss 10.0 − Algèbre linéaire
Systèmes d'équations linéaires
Ce module calcule le vecteur solution d'un système d'équations linéaires comportant n équations à n inconnues.
Exemple : La recherche d'une parabole passant par les points P(1|3), Q(2|1) et R(4|9) conduit au système suivant :
1·x1 + 1·x2 + 1·x3 = 3
4·x1 + 2·x2 + 1·x3 = 1
16·x1 + 4·x2 + 1·x3 = 9
L = (2; -8; 9)
La parabole obtenue a pour équation : y = 2x2 - 8x + 9.
Exemple avec un espace de solutions de dimension 2 :
0·x1 + 0·x2 + 2·x3 - 1·x4 = 1
1·x1 + 1·x2 + 1·x3 + 1·x4 = 4
2·x1 + 2·x2 - 4·x3 + 5·x4 = 5
1·x1 + 1·x2 - 7·x3 + 5·x4 = 0
L = { (3,5 - s - 1,5t; s; 0,5 + 0,5t; t) | s, t ∈ R }
 Optimisation linéaire
(depuis février 2022)
Optimisation linéaire
(depuis février 2022)
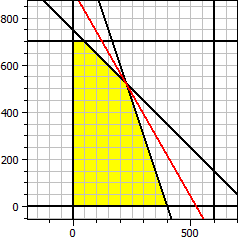
Ce module détermine la solution optimale d'une fonction objectif à deux variables sous contraintes.
Fonction objectif : ƒ(x, y) = 140·x + 80·y → Maximum Contraintes : x ≥ 0 y ≥ 0 x ≤ 600 y ≤ 700 x + y ≤ 750 3·x + y ≤ 1200 Solution optimale : x = 225 y = 525 ƒ(x, y) = 73500
 Combinaisons linéaires
Combinaisons linéaires
Ce module calcule la combinaison linéaire d'un vecteur à partir de trois vecteurs indépendants donnés.
⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 2 ⎫
a·⎪ 0 ⎪ + b·⎪ 1 ⎪ + c·⎪ 1 ⎪ = ⎪ 3 ⎪
⎩ 0 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭ ⎩ 4 ⎭
Solution :
a = -1 b = -1 c = 4
 Produit scalaire
Produit scalaire
Ce module calcule le produit scalaire de deux vecteurs, leurs longueurs et l'angle entre eux.
-> ⎧ 1 ⎫ -> ⎧ 5 ⎫
a = ⎪ 3 ⎪ b = ⎪ 0 ⎪
⎩ 1 ⎭ ⎩ 3 ⎭
Produit scalaire = 8
Longueur du 1er vecteur = √11 = 3,32
Longueur du 2e vecteur = √34 = 5,83
Angle entre les vecteurs α = 65,56°
 Produit vectoriel
Produit vectoriel
Ce module calcule le produit vectoriel de deux vecteurs et sa norme.
Le vecteur obtenu est perpendiculaire au parallélogramme formé et sa norme correspond à l'aire de ce parallélogramme.
-> ⎧ 1 ⎫ -> ⎧ 7 ⎫
a = ⎪ 2 ⎪ b = ⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 4 ⎭
-> -> ⎧ 5 ⎫ -> ->
a x b = ⎪ 17 ⎪ |a x b|= √483 = 21,977261
⎩-13 ⎭
 Produit triple
Produit triple
Ce module calcule le produit triple de trois vecteurs.
Sa valeur représente le volume du parallélépipède défini par ces vecteurs.
→ ⎧ 2 ⎫ → ⎧ 2 ⎫ → ⎧ 3 ⎫
a = ⎪ 3 ⎪ b = ⎪-1 ⎪ c = ⎪ 9 ⎪
⎩ 5 ⎭ ⎩ 7 ⎭ ⎩ 2 ⎭
( a × b ) · c = 26
 Inversion de matrices
Inversion de matrices
Ce module calcule l'inverse d'une matrice carrée, ainsi que son rang et son déterminant.
Matrice : ⎧ 1 0 2 ⎫ ⎪ 0 1 0 ⎪ ⎩ 3 0 1 ⎭ Matrice inverse : ⎧-0,2 0 0,4 ⎫ ⎪ 0 1 0 ⎪ ⎩ 0,6 0 -0,2 ⎭ Ordre = 3 Rang = 3 Déterminant = -5
 Matrice pseudo inverse
Matrice pseudo inverse
Si les colonnes d'une matrice A sont linéairement indépendants, alors
A+ = (AT · A)-1 · AT
A+ est une inverse à gauche de A ,
ce qui signifie que:
Matrix A ¯¯¯¯¯¯¯¯ ⎧ 1 1 1 1 ⎫ ⎩ 5 7 7 9 ⎭ AT· A ¯¯¯¯¯ ⎧ 26 36 36 46 ⎫ ⎪ 36 50 50 64 ⎪ ⎪ 36 50 50 64 ⎪ ⎩ 46 64 64 82 ⎭ AT· A singulière A · AT ¯¯¯¯¯¯ ⎧ 4 28 ⎫ ⎩ 28 204 ⎭ ( A · AT )-1 ¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 6,375 -0,875 ⎫ ⎩-0,875 0,125 ⎭ Inverse à droite: AT·( A·AT )-1 ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 2 -0,25 ⎫ ⎪ 0,25 0 ⎪ ⎪ 0,25 0 ⎪ ⎩ -1,5 0,25 ⎭
 Produit des matrices
Produit des matrices
Le programme calcule le produit des deux matrices.
1e Matrice : ¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 1 0 2 ⎫ ⎩ 0 1 0 ⎭ 2e Matrice : ¯¯¯¯¯¯¯¯¯¯¯¯ ⎧-0,2 0 0,4 1 ⎫ ⎪ 0 1 0 1 ⎪ ⎩ 0,6 0 -0,2 1 ⎭ Produit des Matrices: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ⎧ 1 0 0 3 ⎫ ⎩ 0 1 0 1 ⎭

