Kreistangenten-Berechnung
Pol und Polare
Der Kreis k um den Mittelpunkt M mit Radius r wird beschrieben durch die Gleichung
( x - xM)2 + ( y - yM)2 = r2.
Setzt man bei den beiden Quadraten auf der linken Seite jeweils in einem Faktor für x bzw. y
die Koordinaten des Punktes P ein, so erhält man die folgende Gleichung, die eine Gerade beschreibt.
( xP - xM)·( x - xM) + ( yP - yM )·( y - yM ) = r2.
Sie wird Polare zum Pol P genannt und ist ein starkes Hilfsmittel bei der Bestimmung der Tangentengleichungen.
Die Tangenten an einen Kreis k durch einen Punkt P
Sind ein Kreis k und ein Punkt P auf dem Kreis gegeben, so ist die Polare von P die gesuchte Tangente
Sind ein Kreis k und ein Punkt P außerhalb von k gegeben, so schneidet die Polare von P den Kreis in den beiden Berührpunkten der Tangenten durch P. Man löst also die Gleichung der Polare nach y auf (bzw. nach x, falls der Koeffizient von y Null ist) und setzt sie in die Kreisgleichung ein. Mit den so berechneten Berührpunkten B1 und B2 stellt man die Gleichungen der Tangenten t1=(P B1) und t2=(P B2) auf.
Liegt der Punkt P innerhalb des Kreise, so ist die Polare eine Gerade außerhalb des Kreises. Die Punkte auf dieser haben alle die Eigenschaft, dass sich ihre Polaren in P schneiden.
Die Tangenten an einen Kreis k parallel zu einer Geraden g
Sind ein Kreis k und eine Gerade g: a·x + b·y = c gegeben, so schneidet die Lotgerade auf g durch den Mittelpunkt M des Kreises diesen in den Berührpunkten B1 und B2. Für die Koeffizienten der Lotgerade gilt a'=-b und b'=a. Den konstanten Summanden c' erhält man, indem man die Koeffizienten von M einsetzt.
Die Tangenten an zwei Kreise k1 und k2
Sind r1 und r2 die Radien der Kreise k1 und k2, so nehmen wir o.B.d.A. an, dass r1 > r2. Trifft das nicht zu, werden die Kreise getauscht.
Wie viele gemeinsame Tangenten zwei Kreise haben, hängt von der gegenseitigen Lage der Kreise ab:

|M1M2| < r1−r2

|M1M2| = r1−r2

r1−r2 < |M1M2| < r1+r2
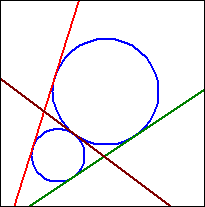
|M1M2| = r1+r2
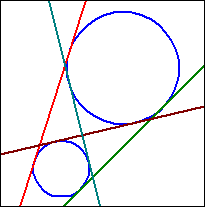
|M1M2| > r1+r2
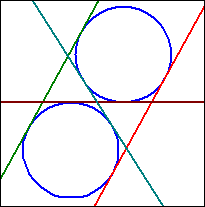
Sonderfall r1 = r2
a) |M1M2| = r1−r2
Den gemeinsamen Berührpunkt B berechnet man am einfachsten indem man zu dem Ortsvektor von M2
das r2/|M1M2|-fache des Vektors von M1 nach M2 addiert.
Die Tangente ist die Lotgerade zu (M1M2) in B.
b) |M1M2| > r1−r2
Um die äußeren Tangenten an zwei Kreise zu bestimmen, bestimmt man zunächst die Tangenten an einen Kreis k3 um M1
mit Radius r3=r1−r2 durch M2 (analog zur Aufgabe Tangente an k durch P).
Sind P1 und P2 die Berührpunkt auf k3, dann verschiebt diese um das r1/r3-fache des Vektors von M1 nach P1 bzw. nach P2 (vgl. a)).
Einen Sonderfall bilden zwei Kreise mit gleich großem Radius, da der Hilfskreis k3 den Radius Null hätte. In diesem Fall bestimmt man die Tangenten analog zur Aufgabe Tangente an k parallel zu g mit g = (M1M2).
c) |M1M2| = r1 + r2
Berühren sich die beiden Kreise von außen, so existiert eine dritte gemeinsame Tangente t3.
Der gemeinsame Berührpunkt teilt die Strecke M1M2 im Verhältnis r1 : r2.
Die Tangente t3 ist orthogonal zu M1M2.
d) |M1M2| > r1 + r2
Liegt k2 ganz außerhalb k1, so existieren zwei "innere" gemeinsame Tangenten, die sich zwischen den
Kreisen kreuzen.
Um die inneren Tangenten an zwei Kreise zu bestimmen, bestimmt man zunächst die Tangenten an einen Kreis k3 um M1
mit Radius r3=r1+r2 durch M2 (analog zur Aufgabe Tangente an k durch P).
Sind P1 und P2 die Berührpunkt auf k3, dann verschiebt man diese um das
r1/r3-fache des Vektors von M1 nach P1 bzw. nach P2 (vgl. a)).
Siehe auch:
Einstellen der Grafik
Wikipedia: Kreistangente |
Pol und Polare

