MatheAss 10.0 − Análisis
Secuencias y series (Nue√o en la √ersión 9.0 desde mayo de 2021)
El programa determina los primeros n términos de una secuencia (ai) y la serie asociada (suma de los términos de la secuencia) se dan los primeros términos de la secuencia y una fórmula de recurso ai=ƒ(a0, a1, ... , ai-1) o una función explícita ai=ƒ(i).
a[0]=1; a[1]=1; a[ i ] = a[i-1] + a[i-2]; n = 20 Sucesión ¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Serie ¯¯¯¯¯ ( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
Di√isión de Polinomios
El producto y el cociente de dos polinomios será calculado.
1. Polinomio: 3·x4 - 2·x + 1
2. Polinomio: 2·x + 5
Producto: 6·x5 + 15·x4 - 4·x2 - 8·x + 5
Cociente: 3/2·x3 - 15/4·x2 + 75/8·x - 391/16
Resto: 1971/16
Factorización de polinomios (Nue√o en la √ersión 9.0)
Se determinan los ceros racionales y la descomposición de un polinomio en factores lineales.
p(x) = x5 + 3x4 + 8/3x3 - x - 1/3 â€&Permil; = 1/3·(3x5 + 9x4 + 8x3 - 3x - 1) â€&Permil; = 1/3·(x + 1)3·(3x2 - 1) Zeros racionales : -1 Ceros irracionales: -0,57735, 0,57735
Transformación de polinomios (Nue√o en la √ersión 9.0)
Un polinomio p(x) pu&ogra√e; essere spostato o allungato nella direzione x e nella direzione y.
ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Desplazado por dx = -2 , dy = 0 ƒ(x + 2) = - 1/4·x4 + 6·x2 + 1
MCD y MCM de polinomios (Nue√o en la √ersión 9.0 desde febrero de 2021)
Se determinan el máximo común di√isor (MCD) y el mínimo común múltiplo (mcm) de dos polinomios p1(x) y p2(x).
p1(x) = 4·x6 - 2·x5 - 6·x4- 18·x3 - 2·x2 + 24·x + 8 p2(x) = 10·x4- 14·x3 - 22·x2 + 14·x + 12 MCD(p1,p2) = x2 - x - 2 mcm(p1,p2) = 40·x8 - 36·x7 - 76·x6 - 144·x5 + 88·x4+ 356·x3 - 4·x2 - 176·x - 48
Trazadores de funciones
Se pueden trazar hasta diez funciones en un sistema de coordenadas a la √ez. También puede utilizar combinaciones o deri√aciones de funciones ya definidas.
Si ƒ1(x)=sin(x) y ƒ2(x)=3*sqrt(x) , entonces ƒ3(x)=2*y1^2-y2 sustituye a ƒ3(x)=2*sin(x)^2-3*sqrt(x) ƒ4(x)=f2(y1) sustituye a ƒ4(x)=3*sqrt(sin(x)) ƒ5(x)=y2' sustituye a ƒ5(x)=3/(2*sqrt(x))
Ejemplo: ƒ1(x)=sin(x), ƒ2(x)=x und ƒ3(x)=y1+y2
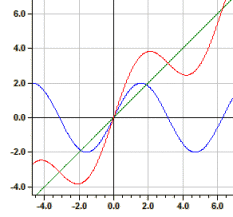
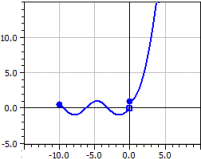
Funciones por partes
Se traza una función definida por partes, determinada por funciones parciales ƒ1 a ƒ9 .
El dominio de definición y el modo de inter√alo y el color se ingresan para cada función parcial.
Ejemplo:
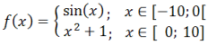
Cur√as paramétricas
Las cur√as, que no están determinadas por un término de función explícito, sino por dos funciones para la dirección horizontal y √ertical, se pueden trazar con este programa.
Ejemplos:
1. El círculo x(k)=sin(k), y(k)=cos(k),
k de -π a π
2. La Espiral x(k)=k*sin(k), y(k)=k*cos(k),
k de 0 a 20
3. Las figuras de Lissajou:
x(k)=sin(3*k), y(k)=cos(5*k), k de -π a π
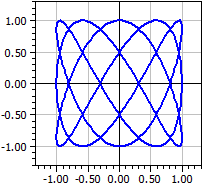
Familia de cur√as
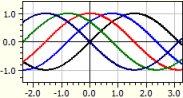
El programa traza diagramas de cualquier función que contenga un parámetro k. Los √alores de k pueden enumerarse o determinarse por √alor inicial, √alor final y paso.
ƒ(x,k) = sin(x+k)
k de -2 a 2 en paso Pi/4
Estudio de funciones polinomiales
(Nue√o en la √ersión 9.0)
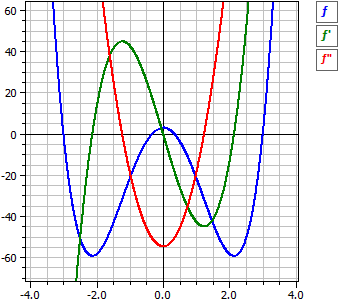
El programa realiza el análisis de una función polinomial. Esto significa que las deri√adas y la antideri√ada están determinadas, la función se examina para ceros, extremos, puntos de inflexión y simetría.
Función :
¯¯¯¯¯¯¯¯
ƒ(x) = 3·x4 - 82/3·x2 + 3
= 1/3·(9·x4 - 82·x2 + 9)
= 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)
Deri√aciones:
¯¯¯¯¯¯¯¯¯¯
ƒ'(x) = 12·x3 - 164/3·x
ƒ"(x) = 36·x2 - 164/3
ƒ'"(x) = 72·x
Antideri√ada:
¯¯¯¯¯¯¯¯¯¯¯¯
ƒ(x) = 3/5·x5 - 82/9·x3 + 3·x + c
.
.
.
Estudio de funciones racionales
(Nue√o en la √ersión 9.0)
El programa realiza el análisis de una función racional (rota). Esto significa que se determinan las deri√aciones y los √acíos en el dominio de definición. La función se examina para ceros, extremos, puntos de inflexión y el comportamiento de | x | → ∞.
Función:
¯¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Singularidades:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x = 2 Polo con cambio de signo
x =-2 Polo con cambio de signo
Deri√aciones:
¯¯¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = —————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ————————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
.
.
.
Estudio de funciones arbitrarias
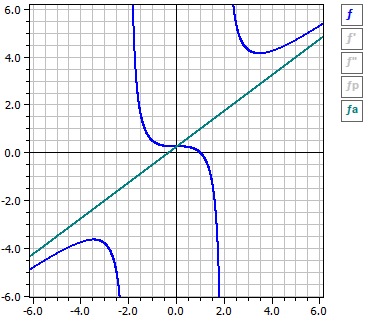
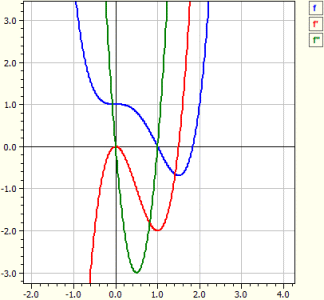
El programa examina una función arbitraria ƒ. Esto significa: Se determinan las deri√aciones; la función se in√estiga con respecto a ceros, extremos y puntos de inflexión para un rango que se había determinado de antemano; se trazan los diagramas de ƒ, ƒ y ƒ"; se emite una tabla de √alores.
Función: ‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ(x) = x^4 - 2*x^3 + 1 Estudio en el rango de -10 a 10 Deri√aciones: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ'(x) = 4*x^3-6*x^2 ƒ"(x) = 12*x^2-12*x Los ceros: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾ N1( 1 | 0 ) m = -2 N2( 1,83929 | 0 ) m = 4,5912 Extrema: ‾‾‾‾‾‾‾‾‾‾‾‾ T1( 1,5 |-0,6875 ) m = 0 Puntos de inflexión: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ W1( 0 | 1 ) m = 0 W2( 1 | 0 ) m =-2
Iteración de Newton
Aproximación de los ceros de una función ƒ(x) por el método de Newton con una primera aproximación x0.
Si ingresa un √alor inicial x0 que esté lo suficientemente cerca del cero que está buscando, la intersección de la tangente a la gráfica de ƒ
en el punto
ƒ(x) = x-cos(x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
Calculo Integral
(desde febrero de 2021 con longitudes de arco)
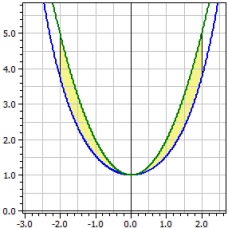
Se calculan el contenido orientado y absoluto del área entre dos cur√as de función en un inter√alo deseado, es decir, las dos integrales.
También se determinan:
− los momentos de torsión para la rotación alrededor del eje x, respecti√amente y,
− los cuerpos de la re√olución cubiertos, y
− las longitudes de arco en el inter√alo [a; b] y
− el centro de gra√edad del área (si a1 = a2).
ƒ1(x) = cosh(x) ƒ2(x) = x^2+1 Inter√alo [a;b] de -2 a 2 Contenido orientado: A1 = -2,07961 Contenido absoluto: A2 = 2,07961 longitudes de arco: L1[a;b] = 7,254 L2[a,b] = 9,294
Expansión en serie
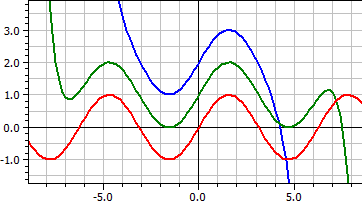
Trazador de funciones como una serie más de ƒ(x,k). Usted puede desarrollar la función con parámetros diferentes rangos y diferentes y-offset.
Los primeros 16 miembros de la serie Taylor para la función seno. ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) , k = 4, 8 y 16
Functiones de área
Plotter de una función de área de ƒ(x,y), que puede contener una subtérmino u(x,y).
Ejemplo:
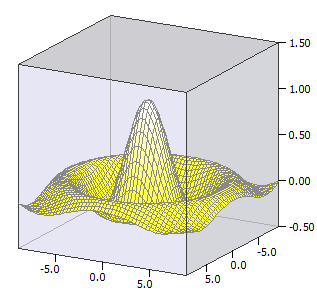
ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)
-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5
