MatheAss 10.0 − Algebra

Primzahlen

Das Programm berechnet alle Primzahlen zwischen zwei Zahlen.

Primzahlen zwischen 1000000000 und 1000000300:

1000000007 1000000009 1000000021 1000000033 1000000087 1000000093
1000000097 1000000103 1000000123 1000000181 1000000207 1000000223
1000000241 1000000271 1000000289 1000000297

16 Primzahlen

Primzahltupel (Neu in Version 9.0)

Das Programm bestimmt in einem Intervall [a,b] alle Primzahlzwillinge (p,p+2), Primzahlcousins (p,p+4), Sexy Primes (p,p+6) und Primzahldrillinge.

Primzahldrillinge zwischen 1 und 200

(3|5|7) (5|7|11) [7|11|13] (11|13|17) [13|17|19] (17|19|23) [37|41|43] 
(41|43|47) [67|71|73] [97|101|103] (101|103|107) [103|107|109] (107|109|113)
(191|193|197) [193|197|199] 

15 Tripel Primzahldrillinge
7 der Form (p|p+2|p+6) und 7 der Form [p|p+4|p+6]

Primfaktorzerlegung

Das Programm zerlegt natürliche Zahlen in ihre Primzahlpotenzen.

  99999999999901 = 19001 · 5262880901
  99999999999001 = 107 · 401 · 1327 · 1756309
  99999999990001 = Primzahl 
    3938980639167 = 3¹⁴ · 7⁷
999330136292431 = 99971² · 99991

ggT und kgV

Zu zwei Zahlen a und b werden der größte gemeinsame Teiler, das kleinste gemeinsame Vielfache und ihre Teilermengen bestimmt.

a = 24
b = 256

größter gemeinsamer Teiler               ggT = 8
kleinstes gemeinsames Vielfaches    kgV = 768  

Teilermengen :
T(a) = { 1 2 3 4 6 8 12 24}
T(b) = { 1 2 4 8 16 32 64 128 256}

Prozentrechnen (Neu in Version 9.0)

Berechnet werden der Grundwert G, der Prozentwert W, der Prozentsatz p bzw. p%, der Wachstumsfaktor q und der Endwert E, wenn zwei unabhängige davon eingegeben werden.

Gegeben:
¯¯¯¯¯¯¯¯
        Prozentwert  W = −120
Wachstumsfaktor  q = 95% = 0,95 = 19/20

Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
          Grundwert  G = 2400
     Prozentsatz  p% = −5% = −0,05 = −1/20      
              Endwert  E = 2280

Dezimalzahlen in Brüche

Das Programm wandelt periodische und abbrechende Dezimalbrüche in Brüche um.

Nichtperiodischer Teil : 1.20
Periode : 045
    ___
1.20045 = 120/100 + 1/2220 = 533/444

Brüche in Dezimalzahlen

Das Programm wandelt Brüche in periodische Dezimalbrüche um und bestimmt die Periode und ihre Länge.

Zähler : 533
Nenner : 444
              ___
533/444 = 1.20045
periodisch ab der 3. Stelle nach dem Komma
die Periode ist 3 Ziffern lang

Binome

Zu den bekanntesten Formeln der Schulmathematik gehört sicher die binomische Formel (a + b)² = a² + 2ab + b² .

Das Programm berechnet den allgemeineren Fall (a·x + b·y)ⁿ.

(2·x  − 3·y)⁷ =       +128 · x⁷
                           −1344 · x⁶ · y
                            +6048 · x⁵ · y²
                          −15120 · x⁴ · y³   
                          +22680 · x³ · y⁴
                          −20412 · x² · y⁵
                          +10206 · x · y⁶
                            −2187 · y⁷

Das Programm bestimmt die reellwertigen Lösungen einer Gleichung 4. oder kleineren Grades. Für Gleichungen höheren Grades gibt es abgesehen von Näherungsrechnungen (Nullstellen im Progr. Kurvendiskussion) kein algebraisches Lösungsverfahren.

x⁴ + 2·x³ - 3·x² + 5·x - 5 = 0   <=>   (x - 1)·(x³ + 3·x² + 5) = 0
L = {-3,42599;  1}

Diophantische Gleichungen

Benannt nach Diophantos von Alexandria (um 250), der in seinem Buch Arithmetica das Lösen linearer und quadratischer Gleichungen, insbesondere deren ganzzahlige Lösungen behandelt.
Das Programm berechnet die ganzzahligen Lösungen der Gleichung a·x - b·y - c = 0. Damit lassen sich die ganzzahligen Punkte auf einer Geraden bestimmen.

7·x − 3·y − 5 = 0 ;   x,y ganzzahlig
L = { ( 2 + 3t | 3 + 7t ) }

Pythagoräische Zahlentripel

Pythagoräische Zahlentripel sind die ganzzahligen Lösungen (x,y,z) der Gleichung x² + y² = z² , die für die Seiten in rechtwinkligen Dreiecken gilt.

Für x, y, z zwischen 100 und 400 erhält man:

( 119, 120, 169 )    ( 104, 153, 185 )    ( 133, 156, 205 )    ( 105, 208, 233 )    
( 140, 171, 221 )    ( 115, 252, 277 )    ( 120, 209, 241 )    ( 161, 240, 289 )    
( 160, 231, 281 )    ( 207, 224, 305 )    ( 175, 288, 337 )    ( 135, 352, 377 )    
( 136, 273, 305 )    ( 204, 253, 325 )    ( 225, 272, 353 )    ( 189, 340, 389 )    
( 180, 299, 349 )    ( 252, 275, 373 )    ( 152, 345, 377 )    ( 228, 325, 397 )

Taschenrechner

Es gibt vier Taschenrechner:

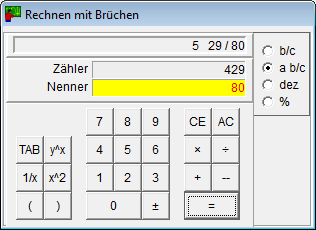
Der Taschenrechner für Brüche beherrscht die vier Grundrechenarten und kann potenzieren.
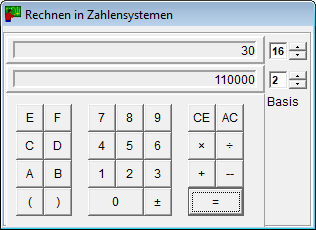
Der Taschenrechner für Stellenwertsysteme rechnet mit jeder Basis zwischen 2 und 16.
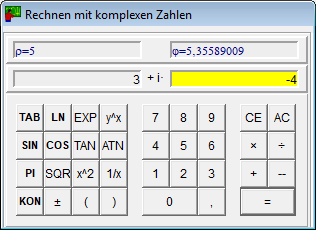
Der Taschenrechner für komplexe Zahlen berechnet außer den üblichen Funktionen auch die Konjugiert Komplexen einer Zahl.
Der Taschenrechner für große ganze Zahlen beherrscht die Grundrechenarten und die Formeln der Kombinatorik.

Rechnen mit großen Zahlen (Neu in Version 9.0 ab April 2021)

Gerechnet wird mit ganzen Zahlen mit maximal 10 000 Ziffern.

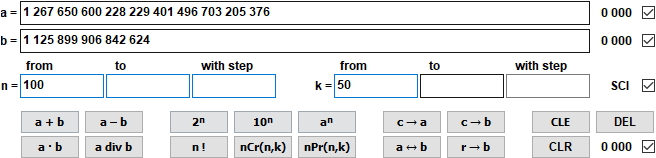
1 267 650 600 228 229 401 496 703 205 376   div  1 125 899 906 842 624  
 =  1 125 899 906 842 624  Rest  0
 =  1,13 · 10^15 Rest 0

nCr(100,50)  =  100 891 344 545 564 193 334 812 497 256 = 1,01 · 10^29