MatheAss 10.0 − Algebra

Primtal

Programmet beräknar alla primtal mellan två tal.

Primtal mellan 1000000000 och 1000000300:

1000000007 1000000009 1000000021 1000000033 1000000087 1000000093
1000000097 1000000103 1000000123 1000000181 1000000207 1000000223
1000000241 1000000271 1000000289 1000000297

16 primtal

Primtalspar   (Nytt i version 9.0)

Programmet bestämmer i ett intervall [a,b] alla primtalstvillingar (p,p+2), primtalskusiner (p,p+4), Sexy Primes (p,p+6) och primtalstrillingar.

Primtalstrillingar mellan 1 och 200

(3|5|7) (5|7|11) [7|11|13] (11|13|17) [13|17|19] (17|19|23) [37|41|43] 
(41|43|47) [67|71|73] [97|101|103] (101|103|107) [103|107|109] (107|109|113)
(191|193|197) [193|197|199] 

15 trillingar av primtal
7 av formen (p|p+2|p+6) och 7 av formen [p|p+4|p+6]

up Primtalsfaktorisering

Programmet faktoriserar naturliga tal i sina primtalspotenser. 

  99999999999901 = 19001 · 5262880901
  99999999999001 = 107 · 401 · 1327 · 1756309
  99999999990001 = primtal 
    3938980639167 = 314 · 77
999330136292431 = 999712 · 99991

up sgd och mgm

För två tal a och b bestäms den största gemensamma delaren, det minsta gemensamma multipeln och deras delmängder. 

a = 24
b = 256

största gemensamma delare               sgd = 8
minsta gemensamma multipel                mgm = 768  

Delmängder :
T(a) = { 1 2 3 4 6 8 12 24}
T(b) = { 1 2 4 8 16 32 64 128 256}

up Procenträkning   (Nytt i version 9.0)

Beräknas blir grundvärde G, procentvärde W, procentsats p respektive p%, tillväxtfaktor q och slutvärde E, när två oberoende av dessa anges.

Givet:
¯¯¯¯¯¯¯¯
        Procentvärde  W = −120
Tillväxtfaktor  q = 95% = 0,95 = 19/20

Resultat:
¯¯¯¯¯¯¯¯¯¯
          Grundvärde  G = 2400
     Procentsats  p% = −5% = −0,05 = −1/20      
              Slutvärde  E = 2280

up Decimaltal till bråk

Programmet omvandlar periodiska och avbrytande decimaltal till bråk. 

Icke-periodisk del : 1.20
Period : 045
    ___
1.20045 = 120/100 + 1/2220 = 533/444

up Bråk till decimaltal

Programmet omvandlar bråk till periodiska decimaltal och bestämmer perioden och dess längd. 

Täljar : 533
Nämnare : 444
              ___
533/444 = 1.20045
periodisk från den 3:e positionen efter kommatecknet
perioden är 3 siffror lång

up Binom

Till de mest kända formlerna i skolmatematiken hör säkert den binomiska formeln (a + b)² = a² + 2ab + b² .

Programmet beräknar det mer allmänna fallet (a·x + b·y)n. 

(2·x  − 3·y)7 =       +128 · x7
                           −1344 · x6 · y
                            +6048 · x5 · y2
                          −15120 · x4 · y3   
                          +22680 · x3 · y4
                          −20412 · x2 · y5
                          +10206 · x · y6
                            −2187 · y7

up Ekvationer av 4:e graden

Programmet bestämmer de reella lösningarna till en ekvation av 4:e eller lägre graden. För ekvationer av högre grad finns, bortsett från närmeberäkningar (nollställen i progr. funktionsanalys), inget algebraiskt lösningsförfarande. 

x4 + 2·x3 - 3·x2 + 5·x - 5 = 0   <=>   (x - 1)·(x3 + 3·x2 + 5) = 0
L = {-3,42599;  1}

up Diofantiska ekvationer

Uppkallade efter Diophantos från Alexandria (omkring 250), som i sin bok Arithmetica behandlade lösningen av linjära och kvadratiska ekvationer, särskilt deras heltalslösningar.
Programmet beräknar heltalslösningarna till ekvationen  a·x - b·y - c = 0. Därmed kan de heltalspunkter på en linje bestämmas. 

7·x − 3·y − 5 = 0 ;   x,y heltal
L = { ( 2 + 3t | 3 + 7t ) }

up Pythagoreiska taltripplar

Pythagoreiska taltripplar är de heltalslösningar (x,y,z) till ekvationen x² + y² = z² , som gäller för sidorna i rätvinkliga trianglar.

För x, y, z mellan 100 och 400 får man:

( 119, 120, 169 )    ( 104, 153, 185 )    ( 133, 156, 205 )    ( 105, 208, 233 )    
( 140, 171, 221 )    ( 115, 252, 277 )    ( 120, 209, 241 )    ( 161, 240, 289 )    
( 160, 231, 281 )    ( 207, 224, 305 )    ( 175, 288, 337 )    ( 135, 352, 377 )    
( 136, 273, 305 )    ( 204, 253, 325 )    ( 225, 272, 353 )    ( 189, 340, 389 )    
( 180, 299, 349 )    ( 252, 275, 373 )    ( 152, 345, 377 )    ( 228, 325, 397 )

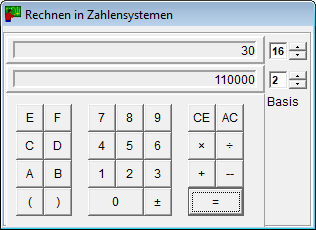
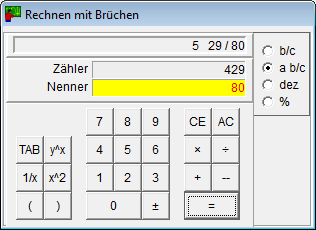
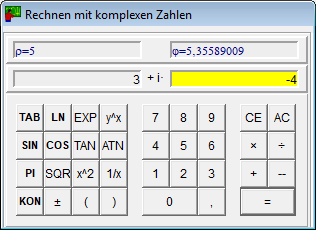
up Miniräknare

Det finns fyra miniräknare:

  • Miniräknaren för bråk behärskar de fyra räknesätten och kan upphöja i potens.
  • Miniräknaren för positionssystem räknar med varje bas mellan 2 och 16.
  • Miniräknaren för komplexa tal beräknar förutom de vanliga funktionerna även det konjugerade komplexa av ett tal.
  • Miniräknaren för stora heltal behärskar de grundläggande räknesätten och kombinatorikens formler.
TR TR TR

Beräkning med stora tal (Nytt i version 9.0 från april 2021)

Beräkningen sker med heltal med maximalt 10 000 siffror.

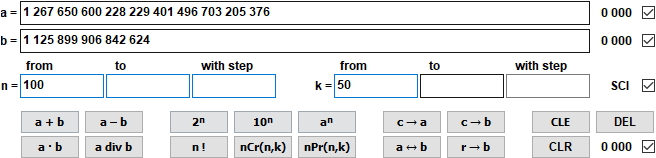
1 267 650 600 228 229 401 496 703 205 376   div  1 125 899 906 842 624  
 =  1 125 899 906 842 624  Rest  0
 =  1,13 · 10^15 Rest 0

nCr(100,50)  =  100 891 344 545 564 193 334 812 497 256 = 1,01 · 10^29