MatheAss 10.0 − Stokastik

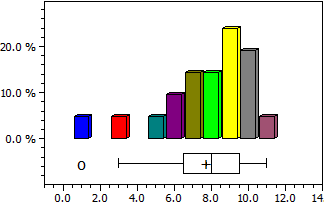
Statistik

För en ursprungslista beräknas medelvärdet (aritmetiskt medel), medianen, variansen och standardavvikelsen. Dessutom visas fördelningen som histogram och box-plot.

Data:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8

Antal data                   n = 21
Maximum               max = 11
Minimum                 min = 1
Medelvärde                 x = 7,7142857
Median                        c = 8
Varians                       s² = 6,1142857
Standardavvikelse       s = 2,4727082

Regression

Med denna rutin kan du utföra en kurvanpassning till en mätserie. Du kan välja mellan följande anpassningar och vid behov flytta eller skala alla punkter i x- eller y-riktning.

Ursprungslinje ( y = a·x )

Linjär regression ( y = a·x + b )

Polynomregression av n-te ordningen ( y = a₀ + ... + a_n·xⁿ )

Geometrisk regression ( y = a·x^b )

Exponentiell regression ( y = a·b^x )

Logaritmisk regression ( y = a + b·ln(x) )

Tillsammans med diagrammet visas funktionsuttrycket för närmefunktionen, bestämdhetsmåttet, korrelationskoefficienten och standardavvikelsen.

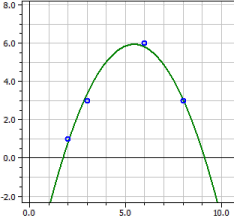
Polynomregression

y =  − 2,6299435
      + 3,8516949·x
      − 0,43361582·x²

Bestämdhetsmått        = 0,98338318
Korrelationskoefficient = 0,99165679        
Standardavvikelse       = 0,46028731

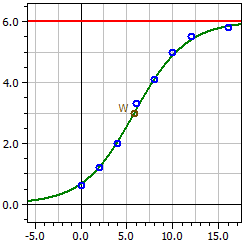
Logistisk regression (Nytt i version 9.0)

Programmet bestämmer för en mätserie en kurvanpassning till den logistiska funktionen
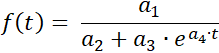
med parametrarna a₁ = ƒ(0)·S , a₂ = ƒ(0) , a₃ = S - ƒ(0) , och a₄ = -k·S samt mättnadsgränsen S .

Data från: "Hopfenwachstum.csv"

Mättnadsgräns: 6
         Mörk siffra: 1

                                 4,0189
ƒ(x) = ————————————————
             0,66981 + 5,3302 · e^(-0,35622·t)

Vändpunkt W(5,8226/3)

Maximal tillväxthastighet  ƒ'(xw) = 0,53433

8 värden 
Bestämdhetsmått        = 0,99383916
Korrelationskoefficient = 0,99691482
Standardavvikelse       = 0,16172584

Kombinatorik

Beräknar antalet möjligheter att välja ut k element från n, beroende på om ordningen spelar roll eller inte och om upprepningar är tillåtna eller inte.

n = 49 ,  k = 6

Ordnat urval utan upprepn.   = 10 068 347 520
Ordnat urval med upprepn.   = 13 841 287 201
Oordnat urval utan upprepn. = 13 983 816
Oordnat urval med upprepn. = 25 827 165

Permutationer av k :                k ! = 720

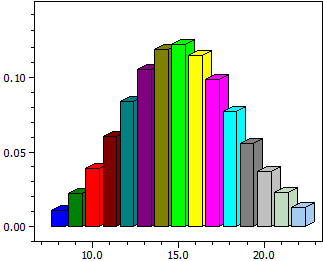
Binomialfördelning

Beräknas för en b(k;n;p)-fördelad slumpvariabel X vid fast n och fast p

- ett stapeldiagram för sannolikheterna P( X = k )
- dess numeriska värden i ett intervall [k-min;k-max]
- sannolikheten P( k-min <= X <= k-max)

n = 50             p = 0,3

    k             P(X=k)         P(0<=X<=k) 
  ¯¯¯¯    ¯¯¯¯¯¯¯¯¯¯     ¯¯¯¯¯¯¯¯¯¯
    8         0,01098914     0,01825335
    9         0,02197829     0,04023163
  10        0,03861899     0,07885062
  11        0,06018544     0,13903606
  12        0,08382972     0,22286578
  13        0,10501745     0,32788324
  14        0,11894834     0,44683157
  15        0,12234686     0,56917844
  16        0,11470018     0,68387862
  17        0,09831444     0,78219306
  18        0,07724706     0,85944012
  19        0,05575728     0,91519740
  20        0,03703876     0,95223616
  21        0,02267679     0,97491296
  22        0,01281092     0,98772387
  ¯¯¯¯    ¯¯¯¯¯¯¯¯¯¯     ¯¯¯¯¯¯¯¯¯¯
  P(8<=k<=22) =            0,98045967

Hypergeometrisk fördelning

Beräknas för en h(k;n;m;r)-fördelad slumpvariabel X vid fast n, m och fast r ett stapeldiagram och en värdetabell för sannolikheterna P( X = k ).

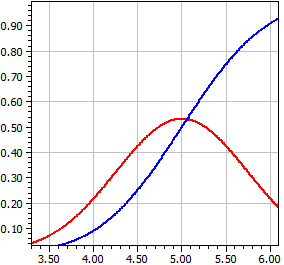
Normalfördelning

Beräknas för en N(µ,σ²)-fördelad slumpvariabel X med givet förväntningsvärde µ och varians σ² densitetsfunktionen ƒ(x) och fördelningsfunktionen Φ(x), det vill säga integralen över ƒ(x) .

  μ = 5              σ = .75

      x                      ƒ(x)                Φ(x)   
  ¯¯¯¯¯¯¯¯¯¯  ¯¯¯¯¯¯¯¯¯¯  ¯¯¯¯¯¯¯¯¯¯
  2                    0,00017844   0,00003167
  2,33333333   0,00095649   0,00018859
  2,66666666   0,00420802   0,00093192
  2,99999999   0,01519465   0,00383038
  3,33333332   0,04503153   0,01313415
  3,66666665   0,10953585   0,03772017
  3,99999998   0,21868009   0,09121120
  4,33333331   0,35832381   0,18703139
  4,66666664   0,48189843   0,32836063
  4,99999997   0,53192304   0,49999998
  5,3333333     0,48189845   0,67163934
  5,66666663   0,35832383   0,81296859
  5,99999996   0,21868012   0,90878878
  6,33333329   0,10953586   0,96227982
  6,66666662   0,04503154   0,98686585
  6,99999995   0,01519465   0,99616962
  7,33333328   0,00420802   0,99906808
  7,66666661   0,00095649   0,99981141
  7,99999994   0,00017844   0,99996833