MatheAss 10.0 − Analys

Följder och serier (Nytt i version 9.0 från maj 2021)

Programmet bestämmer de första n termerna i en följd (a_i) och den tillhörande serien (summan av följdtermerna), när de första termerna i följden och en explicit funktion a_i=ƒ(i) eller en rekursionsformel a_i=ƒ(a₀, a₁, ... , a_i-1) ges.

a[0]=1;   a[1]=1;   a[ i ] = a[i-1] + a[i-2];   n = 20

Följd
¯¯¯¯¯
( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765)

Serie
¯¯¯¯¯
( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)

Polynomdivision

Programmet beräknar produkten och kvoten av två polynom.

1. Polynom:  3·x⁴ - 2·x + 1
2. Polynom:  2·x + 5

      Produkt:  6·x⁵ + 15·x⁴ - 4·x² - 8·x + 5                 
     Kvot:  3/2·x³ - 15/4·x² + 75/8·x - 391/16
           Rest:  1971/16

Faktorisera polynom (Nytt i version 9.0)

Programmet beräknar de rationella nollställena och linjär faktoruppdelning av ett polynom.

p(x) = x⁵ - 9·x⁴ - 82/9·x³ + 82·x² + x - 9
       = (1/9)·(9·x⁵ - 81·x⁴ - 82·x³ + 738·x² + 9·x - 81)
       = (1/9)·(3·x - 1)·(3·x + 1)·(x - 9)·(x - 3)·(x + 3)

Rationella nollställen: 1/3, -1/3, 9, 3, -3

Transformera polynom (Nytt i version 9.0)

En polynomfunktion ƒ(x) kan förskjutas eller skalas i x-riktning och y-riktning.

ƒ(x) =  - 1/4·x⁴ + 2·x³ - 16·x + 21

Förskjutning med dx = -2 ,  dy = 0                             

ƒ(x + 2) =  - 1/4·x⁴ + 6·x² + 1

Polynom sgd och kgv (Nytt i version 9.0 från februari 2021)

Programmet beräknar den största gemensamma delaren (sgd) och det minsta gemensamma multipeln (kgv) av två polynom p₁(x) och p₂(x).

p₁(x) =  4·x⁶ - 2·x⁵ - 6·x⁴- 18·x³ - 2·x² + 24·x + 8
p₂(x) =  10·x⁴- 14·x³ - 22·x² + 14·x + 12

sgd(p₁,p₂) =  x² - x - 2
kgv(p₁,p₂) =  40·x⁸ - 36·x⁷ - 76·x⁶ - 144·x⁵ + 88·x⁴+ 356·x³ - 4·x² - 176·x - 48

Funktionsplotter 1

Upp till tio funktioner kan samtidigt ritas i ett koordinatsystem. Tillåtet är också kombinationer eller derivator av redan definierade funktioner.

Antag  ƒ₁(x)=sin(x) och ƒ₂(x)=3*sqrt(x), då ersätts

ƒ₃(x)=2*y1^2-y2         ƒ₃(x)=2*sin(x)^2-3*sqrt(x)
ƒ₄(x)=f2(y1)               ƒ₄(x)=3*sqrt(sin(x))
ƒ₅(x)=y2'                   ƒ₅(x)=3/(2*sqrt(x))

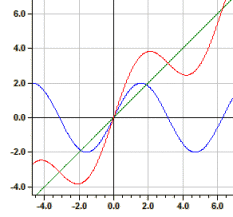
Exempel: ƒ₁(x)=sin(x), ƒ₂(x)=x och ƒ₃(x)=y1+y2

Funktionsplotter 2

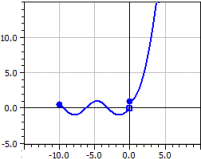
En styckvis definierad funktion ritas, given genom nio delfunktioner. För varje delfunktion anges definitionsmängd, typen av intervall och färgen. Dessutom kan man bestämma om randpunkterna ska ritas eller inte.

Exempel:

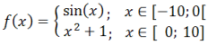
Parameterkurvor

Med detta program kan man rita kurvor som inte ges av en explicit funktionsterm, utan genom två funktioner för den horisontella och vertikala avvikelsen.

Exempel: Lissajous-figurer

x(k) = sin(3*k)

y(k) = cos(5*k)

k från -Pi till Pi

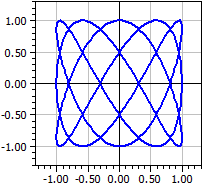
Lissajous-figurer får man när man på ett oscilloskop lägger två växelspänningar med olika frekvens.

Kurvsviter

Programmet ritar grafer för godtyckliga funktioner som innehåller en svitparameter k. Värdena för k kan listas eller bestämmas genom startvärde, slutvärde och steglängd.

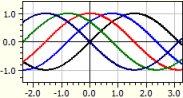
ƒ(x,k) = sin(x+k)

k från -2 till 2 med steglängd Pi/4

Polynomfunktioner (Nytt i version 9.0)

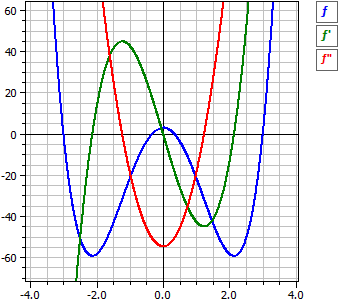
Programmet utför en kurvdiskussion för en helt rationell funktion (polynomfunktion). Det innebär att derivator och stamfunktion (integral) bestäms, samt att funktionen undersöks med avseende på rationella nollställen, extrempunkter, vändpunkter och symmetri.

Funktion :
¯¯¯¯¯¯¯¯
ƒ(x) = 3·x⁴ - 82/3·x² + 3
       = 1/3·(9·x⁴ - 82·x² + 9)
       = 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)                  

Derivator :
¯¯¯¯¯¯¯¯¯¯
ƒ'(x)  = 12·x³ - 164/3·x
ƒ"(x)  = 36·x² - 164/3
ƒ'"(x) = 72·x

Stamfunktion
¯¯¯¯¯¯¯¯¯¯¯¯
ƒ(x) = 3/5·x⁵ - 82/9·x³ + 3·x + c

  .
  .
  .

Rationella funktioner (Nytt i version 9.0)

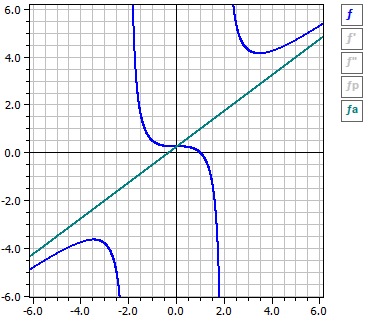
Programmet utför en kurvdiskussion för en (bråk)rationell funktion. Det innebär att derivator, definitionsluckor och den kontinuerliga fortsättningen bestäms. Funktionen undersöks med avseende på nollställen, extrempunkter, vändpunkter och beteendet för |x|→ ∞.

Funktion :
¯¯¯¯¯¯¯¯
            3·x³ + x² - 4         (x - 1)·(3·x² + 4·x + 4)  
ƒ(x) = —————— = ———————————
               4·x² - 16                4·(x - 2)·(x + 2)       

Definitionsluckor
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x = 2  Pol med teckenbyte
x = -2 Pol med teckenbyte

Derivator :
¯¯¯¯¯¯¯¯¯¯
               3·(x⁴ - 12·x²)             3·(x²·(x² - 12))   
ƒ'(x) = ———————— = —————————
            4·(x⁴ - 8·x² + 16)       4·(x - 2)²·(x + 2)² 

                     6·(x³ + 12·x)                6·(x·(x² + 12))  
ƒ"(x) = ——————————— = ————————
             x⁶ - 12·x⁴ + 48·x² - 64        (x - 2)³·(x + 2)³ 

  .
  .
  .

Kurvdiskussion

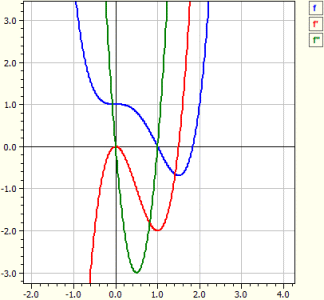
Programmet utför en kurvdiskussion för en godtycklig funktion. Det innebär att derivator bestäms, funktionen undersöks med avseende på nollställen, extrempunkter och vändpunkter, graferna av ƒ, ƒ' och ƒ" ritas, och en värdetabell genereras.

Funktion :
‾‾‾‾‾‾‾‾‾‾‾‾‾
  ƒ(x) = x^4 - 2*x^3 + 1
  Undersökning i intervallet från -10 till 10                

Derivator:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  ƒ'(x) = 4*x^3-6*x^2
  ƒ"(x) = 12*x^2-12*x

Nollställen:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  N₁( 1 | 0 )                  m = -2
  N₂( 1,83929 | 0 )       m =  4,5912

Extrempunkter:
‾‾‾‾‾‾‾‾‾‾‾‾
  T₁( 1,5 |-0,6875 )      m = 0

Vändpunkter:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  W₁( 0 | 1 )                 m = 0
  W₂( 1 | 0 )                 m = -2

Newton-iteration

Newton-iteration är ett närmevärdesförfarande för beräkning av en nollställe till ƒ(x). Om man anger ett startvärde x₀ som ligger tillräckligt nära den sökta nollställen, beräknas som nästa approximation skärningspunkten mellan tangenten till grafen av ƒ i punkten P(x₀ / ƒ(x₀)).

  ƒ(x) = x-cos(x)

                 x                       ƒ(x)                  ƒ'(x) 
   ————————   ——————   ——————   
   x₀ = 1
   x₁ = 0,75036387     0,45969769       1,841471
   x₂ = 0,73911289     0,018923074     1,681905
   x₃ = 0,73908513     0,00004646       1,6736325
   x₄ = 0,73908513     0,00000000       1,673612

Integralkalkyl (från februari 2021 med båglängder)

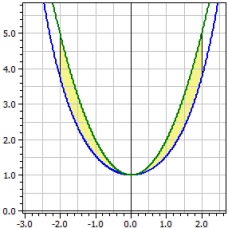
Beräknas är det orienterade och det absoluta innehållet av ytan mellan två funktionskurvor i ett önskat intervall. Dessutom bestäms:
- momenten vid rotation kring x- respektive y-axeln,
- de därvid svepta rotationsvolymerna,
- båglängderna i intervallet [a;b] och
- tyngdpunkten för ytan (när A1=A2).

  ƒ₁(x) = cosh(x)
  ƒ₂(x) = x^2+1

  Integrationsintervall  [a;b]  från  -2 till 2

  Orienterat innehåll :  A₁ = -2,07961
  Absolut innehåll    :  A₂ = 2,07961

  Båglängder       :  L₁[a;b] = 7,254    L₂[a,b] = 9,294

Serieutveckling

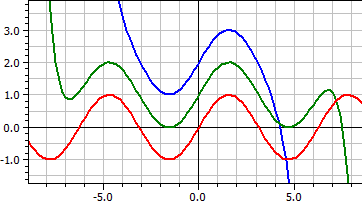
En funktion given som en serie ritas, varvid serieutvecklingarna för olika parameterområden jämförs och för tydligare skillnad kan förskjutas i y-riktning.

De första 16 termerna i Taylorserien 
för sinusfunktionen.

ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) ,   
k = 4, 8 och 16

Ytfunktioner

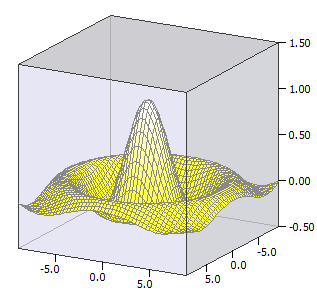
En ytfunktion ƒ(x,y) ritas, det vill säga den tredimensionella grafen av en funktion med två variabler.

Exempel:

ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)

-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5