MatheAss 10.0 − 3-dim. Geometri
Koordinatsystem
Med detta program kan man omvandla tredimensionella kartesiska koordinater till sfärkoordinater eller cylinderkoordinater och omvänt.
kartesisk polar cylindrisk x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Platoniska kroppar
Programmet beräknar de fem platoniska kropparna Tetraeder, Hexaeder, Oktaeder, Dodekaeder och Ikosaeder, när kantlängd, fläkhöjd, rumshöjd, inskriven klotradie, omskriven klotradie, volym eller yta ges.
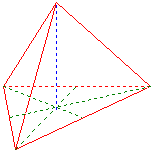
Tetraeder
Givet:
¯¯¯¯¯¯¯¯
Omskriven klotradie ru = 1
Resultat:
¯¯¯¯¯¯¯¯¯¯
Kant a = 1,6329932
Fläkhöjd h1 = 1,4142136
Rumshöjd h2 = 1,3333333
Inskriven klotradie ri = 0,33333333
Volym V = 0,51320024
Yta O = 4,6188022
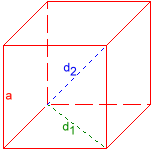
Hexaeder
Givet:
¯¯¯¯¯¯¯¯
Yta O = 8
Resultat:
¯¯¯¯¯¯¯¯¯¯
Kant a = 1,1547005
Fläkdiagonal d1 = 1,6329932
Rumsdiagonal d2 = 2
Omskriven klotradie ru = 1
Inskriven klotradie ri = 0,57735027
Volym V = 1,5396007
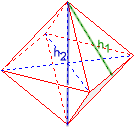
Oktaeder
Givet:
¯¯¯¯¯¯¯¯
Volym V = 4/3
Resultat:
¯¯¯¯¯¯¯¯¯¯
Kant a = 1,4142136
Fläkhöjd h1 = 1,2247449
Rumshöjd h2 = 2
Omskriven klotradie ru = 1
Inskriven klotradie ri = 0,57735027
Yta O = 6,9282032
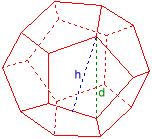
Dodekaeder
Givet:
¯¯¯¯¯¯¯¯
Fläkdiagonal d = 2
Resultat:
¯¯¯¯¯¯¯¯¯
Kant a = 1,236068
Fläkhöjd h = 1,902113
Omskriven klotradie ru = 1,7320508
Inskriven klotradie ri = 1,3763819
Volym V = 14,472136
Yta O = 31,543867
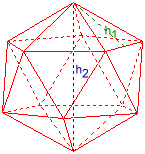
Ikosaeder
Givet:
¯¯¯¯¯¯¯¯
Rumshöjd h2 = 2
Resultat:
¯¯¯¯¯¯¯¯¯
Kant a = 1,0514622
Fläkhöjd h1 = 0,910593
Omskriven klotradie ru = 1
Inskriven klotradie ri = 0,79465447
Volym V = 2,5361507
Yta O = 9,5745414
Övriga kroppar
Programmet beräknar alla storheter för ett regelbundet prisma, en rät cirkelcylinder, en kvadratisk pyramid, en rät cirkelkon eller ett klot, när två av dem ges.
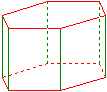
Prismat
Givet: n = 4
¯¯¯¯¯¯¯¯
Volym V = 1
Yta O = 6
Resultat:
¯¯¯¯¯¯¯¯¯
Sida a = 1
Höjd h = 1
Omskriven cirkelradie ru = 0,70710678
Inskriven cirkelradie ri = 0,5
Basarea G = 1
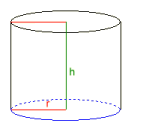
Cylinder
Givet:
¯¯¯¯¯¯¯¯
Radie r = 1
Volym V = 1
Resultat:
¯¯¯¯¯¯¯¯¯¯
Höjd h = 0,31830989
Omkrets u = 6,2831853
Basarea G = 3,1415927
Mantelyta M = 2
Yta O = 8,2831853
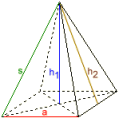
Den kvadratiska pyramiden
Givet:
¯¯¯¯¯¯¯¯
Baslinje a = 1
Volym V = 1
Resultat:
¯¯¯¯¯¯¯¯¯
Sidokant s = 3,082207
Rumshöjd h1 = 3
Sidhojd h2 = 3,0413813
Yta O = 7,0827625
Sidoyta A = 1,5206906
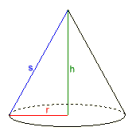
Kon
Givet:
¯¯¯¯¯¯¯¯
Volym V = 1
Basarea G = 1
Resultat:
¯¯¯¯¯¯¯¯¯¯
Radie r = 0,56418958
Höjd h = 3
Mantellinje s = 3,0525907
Mantelyta M = 5,4105761
Yta O = 6,4105761
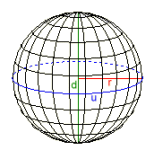
Klotet
Givet:
¯¯¯¯¯¯¯¯
Yta O = 1
Resultat:
¯¯¯¯¯¯¯¯¯¯
Radie r = 0,28209479
Diameter d = 0,56418958
Omkrets u = 1,7724539
Volym V = 0,094031597
Linje genom 2 punkter
Linje A(1|1|1), B(2|5|6)
Parameterframställning
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
x = ⎪ 1 ⎪ + t·⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 5 ⎭
Avstånd från origo
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 0,78679579
Läge till xy-planet
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Ortproj: 4·x - y = 3
Skärnpkt: S1(0,8|0,2|0)
Skärningsvkl: 50,490288°
Läge till yz-planet
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Ortproj: 5·x - 4·y = 1
Skärnpkt: S2(0|-3|-4)
Skärningsvkl: 8,8763951°
Läge till xz-planet
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Ortproj: 5·x - y = 4
Skärnpkt: S3(0,75|0|-0,25)
Skärningsvkl: 38,112927°
Plan genom 3 punkter
Plan genom punkterna:
A(1|2|3), B(2|3|3), C(1|0|1)
Punkt-riktningsform:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
Koordinatform:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Avstånd från origo:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Spårpunkter:
¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)
Klot genom 4 punkter
Klot genom punkterna:
A(1|0|0), B(0|2|0),
C(0|0|3), D(1|0|1)
Normalform:
¯¯¯¯¯¯¯¯¯¯¯
| -> ⎧-2,5 ⎫ |2
K: | x - ⎪-0,5 ⎪ | = 12,75
| ⎩ 0,5 ⎭ |
Mittpunkt och radie:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-2,5|-0,5|0,5)
r = 3,5707142
Snitt i rymden
Programmet beräknar skärningar mellan linjer, plan och klot.
två linjer
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Skärningspunkt : S(5|5|5)
Skärningsvinkel: 60°
Avstånd till origo :
d(O,g)=5 d(O,h)=5
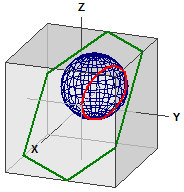
Plan och linje
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
E : x + y + z = 5
Skärningspunkt : S(5|0|0)
Skärningsvinkel: 54,73561°
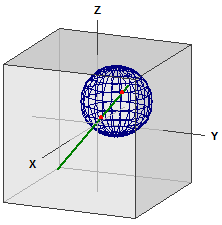
Klot och linje
-> ⎧ 1 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
K : M(5|5|5) , r = 5
Skärningspunkter :
S1(2,8187|1,8187|1,8187)
S2(8,5147|7,5147|7,5147)
Längd av kord :
s = 9,8657657
två plan
Givet är planen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1 : 5·x - 2·y = 5
E2 : 2·x - y + 5·z = 8
Skärningslinje mellan planen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> |-11 | | 10 |
g : x = |-30 | + r·| 25 |
| 0 | | 1 |
Avstånd från origo:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,5057283
Skärningsvinkel mellan planen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 65,993637°
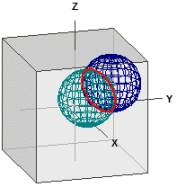
två klot
Givet är kloten: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ K1 : M1(3|3|3) , r1 = 3 K2 : M2(1|1|1) , r2 = 3 Skärningscirkel: ¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2), r = 2,4494897 Skärningsplan: ¯¯¯¯¯¯¯¯¯¯¯¯¯ E : x + y + z = 6
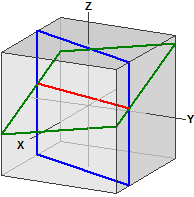
Klot och plan
Plan :
¯¯¯¯¯¯¯
E : 5·x - 4·y + 5·z = -3
Klot :
¯¯¯¯¯¯¯
| -> ⎧ 1 ⎫|2
K : | x - ⎪ 2 ⎪| = 16
| ⎩ 3 ⎭|
Skärningscirkel av K och E :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-0,13636|2,9091|1,8636)
r = 3,548367
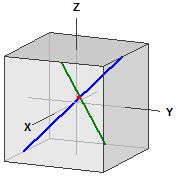
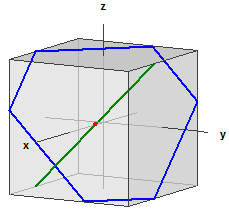
Avstånd på klotet
(Nytt i version 9.0 från december 2021)
Programmet beräknar avståndet mellan två punkter på ett klot. Här sammanfattas flera funktioner i MatheAss.
GPS decimal ¯¯¯¯¯¯¯¯¯¯¯ Berlin : 52.523403, 13.4114 New York : 40.714268, -74.005974 GPS dms ¯¯¯¯¯¯¯ Berlin : 52° 31' 24.2508" N, 13° 24' 41.0400" E New York : 40° 42' 51.3648" N, 74° 0' 21.5064" W . . . Avstånd ¯¯¯¯¯¯¯¯¯¯ d = r · α [rad] = 6385,112
