MatheAss 10.0 − 3-dim. Geometrie
Koordinatensysteme
Mit diesem Programm lassen sich dreidimensionale kartesische Koordinaten in Kugelkoordinaten oder Zylinderkoordinaten umrechnen und umgekehrt.
kartesisch polar zylindrisch x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Platonische Körper
Das Programm berechnet die fünf Platonischen Körper Tetraeder, Hexaeder, Oktaeder, Dodekaeder und Ikosaeder, wenn Kantenlänge, Flächenhöhe, Raumhöhe, Inkugelradius, Umkugelradius, Volumen oder Oberfläche gegeben sind.
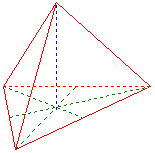
Tetraeder
Gegeben:
¯¯¯¯¯¯¯¯
Umkugelradius ru = 1
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
Kante a = 1,6329932
Flächenhöhe h1 = 1,4142136
Raumhöhe h2 = 1,3333333
Inkugelradius ri = 0,33333333
Volumen V = 0,51320024
Oberfläche O = 4,6188022
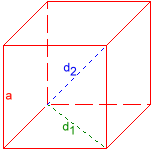
Hexaeder
Gegeben:
¯¯¯¯¯¯¯¯
Oberfläche O = 8
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
Kante a = 1,1547005
Flächendiagonale d1 = 1,6329932
Raumdiagonale d2 = 2
Umkugelradius ru = 1
Inkugelradius ri = 0,57735027
Volumen V = 1,5396007
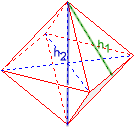
Oktaeder
Gegeben:
¯¯¯¯¯¯¯¯
Volumen V = 4/3
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
Kante a = 1,4142136
Flächenhöhe h1 = 1,2247449
Raumhöhe h2 = 2
Umkugelradius ru = 1
Inkugelradius ri = 0,57735027
Oberfläche O = 6,9282032
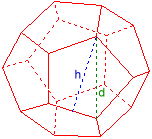
Dodekaeder
Gegeben:
¯¯¯¯¯¯¯¯
Flächendiagonale d = 2
Ergebnisse:
¯¯¯¯¯¯¯¯¯
Kante a = 1,236068
Flächenhöhe h = 1,902113
Umkugelradius ru = 1,7320508
Inkugelradius ri = 1,3763819
Volumen V = 14,472136
Oberfläche O = 31,543867
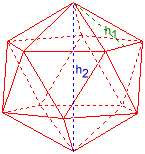
Ikosaeder
Gegeben:
¯¯¯¯¯¯¯¯
Raumhöhe h2 = 2
Ergebnisse:
¯¯¯¯¯¯¯¯¯
Kante a = 1,0514622
Flächenhöhe h1 = 0,910593
Umkugelradius ru = 1
Inkugelradius ri = 0,79465447
Volumen V = 2,5361507
Oberfläche O = 9,5745414
Sonstige Körper
Das Programm berechnet alle Größen eines regelmäßen Prismas, eines senkrechten Kreiszylinders, einer quadratischen Pyramide, eines senkrechten Kreiskegels oder einer Kugel, wenn zwei von ihnen gegeben sind.
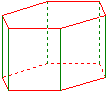
Das Prisma
Gegeben: n = 4
¯¯¯¯¯¯¯¯
Volumen V = 1
Oberfläche O = 6
Ergebnisse:
¯¯¯¯¯¯¯¯¯
Seite a = 1
Höhe h = 1
Umkreisradius ru = 0,70710678
Inkreisradius ri = 0,5
Grundfläche G = 1
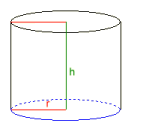
Der Kreiszylinder
Gegeben:
¯¯¯¯¯¯¯¯
Radius r = 1
Volumen V = 1
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
Höhe h = 0,31830989
Umfang u = 6,2831853
Grundfläche G = 3,1415927
Mantelfläche M = 2
Oberfläche O = 8,2831853
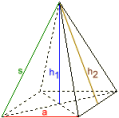
Die quadr. Pyramide
Gegeben:
¯¯¯¯¯¯¯¯
Grundkante a = 1
Volumen V = 1
Ergebnisse:
¯¯¯¯¯¯¯¯¯
Seitenkante s = 3,082207
Raumhöhe h1 = 3
Seitenhöhe h2 = 3,0413813
Oberfläche O = 7,0827625
Seitenfläche A = 1,5206906
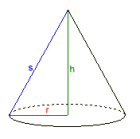
Der Kreiskegel
Gegeben:
¯¯¯¯¯¯¯¯
Volumen V = 1
Grundfläche G = 1
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
Radius r = 0,56418958
Höhe h = 3
Mantellinie s = 3,0525907
Mantelfläche M = 5,4105761
Oberfläche O = 6,4105761
Die Kugel
Gegeben:
¯¯¯¯¯¯¯¯
Oberfläche O = 1
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
Radius r = 0,28209479
Durchmesser d = 0,56418958
Umfang u = 1,7724539
Volumen V = 0,094031597
Gerade durch 2 Punkte
Gerade A(1|1|1), B(2|5|6)
Parameterdarstellung
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
x = ⎪ 1 ⎪ + t·⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 5 ⎭
Abstand vom Ursprung
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 0,78679579
Lage zur xy-Ebene
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
senkr.Proj: 4·x - y = 3
Schnittpkt: S1(0,8|0,2|0)
Schnittwkl: 50,490288°
Lage zur yz-Ebene
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
senkr.Proj: 5·x - 4·y = 1
Schnittpkt: S2(0|-3|-4)
Schnittwkl: 8,8763951°
Lage zur xz-Ebene
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
senkr.Proj: 5·x - y = 4
Schnittpkt: S3(0,75|0|-0,25)
Schnittwkl: 38,112927°
Ebene durch 3 Punkte
Ebene durch die Punkte:
A(1|2|3), B(2|3|3), C(1|0|1)
Punkt-Richtungs-Form:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
Koordinatengleichung:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Abstand vom Ursprung:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Spurpunkte:
¯¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)
Kugel durch 4 Punkte
Kugel durch die Punkte:
A(1|0|0), B(0|2|0),
C(0|0|3), D(1|0|1)
Normalform:
¯¯¯¯¯¯¯¯¯¯¯
| -> ⎧-2,5 ⎫ |2
K: | x - ⎪-0,5 ⎪ | = 12,75
| ⎩ 0,5 ⎭ |
Mittelpunkt und Radius:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-2,5|-0,5|0,5)
r = 3,5707142
Schnitte im Raum
Das Programm berechnet die Schnitte von Geraden, Ebenen und Kugeln.
zwei Geraden
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Schnittpunkt : S(5|5|5)
Schnittwinkel: 60°
Abstände zum Ursprung :
d(O,g)=5 d(O,h)=5
Ebene und Gerade
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
E : x + y + z = 5
Schnittpunkt : S(5|0|0)
Schnittwinkel: 54,73561°
Kugel und Gerade
-> ⎧ 1 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
K : M(5|5|5) , r = 5
Schnittpunkte :
S1(2,8187|1,8187|1,8187)
S2(8,5147|7,5147|7,5147)
Länge der Sehne :
s = 9,8657657
zwei Ebenen
Gegeben sind die Ebenen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1 : 5·x - 2·y = 5
E2 : 2·x - y + 5·z = 8
Schnittgerade der Ebenen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> |-11 | | 10 |
g : x = |-30 | + r·| 25 |
| 0 | | 1 |
Abstand vom Ursprung:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,5057283
Schnittwinkel der Ebenen:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 65,993637°
zwei Kugeln
Gegeben sind die Kugeln: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ K1 : M1(3|3|3) , r1 = 3 K2 : M2(1|1|1) , r2 = 3 Schnittkreis: ¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2), r = 2,4494897 Schnittebene: ¯¯¯¯¯¯¯¯¯¯¯¯¯ E : x + y + z = 6
Kugel und Ebene
Ebene :
¯¯¯¯¯¯¯
E : 5·x - 4·y + 5·z = -3
Kugel :
¯¯¯¯¯¯¯
| -> ⎧ 1 ⎫|2
K : | x - ⎪ 2 ⎪| = 16
| ⎩ 3 ⎭|
Schnittkreis von K und E :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-0,13636|2,9091|1,8636)
r = 3,548367
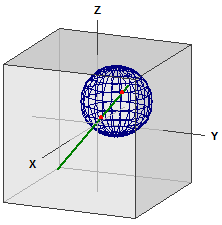
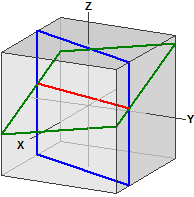
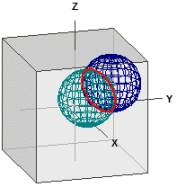
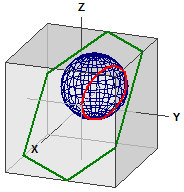
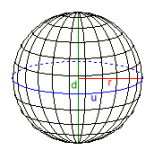
Entfernungen auf der Kugel
(Neu in Version 9.0 ab Dezember 2021)
Berechnet wird die Entfernung zwischen zwei Punkten auf einer Kugel. Dabei werden eine Reihe von Funktionen von MatheAss zusammengefasst.
GPS dezimal ¯¯¯¯¯¯¯¯¯¯¯ Berlin : 52.523403, 13.4114 New York : 40.714268, -74.005974 GPS dms ¯¯¯¯¯¯¯ Berlin : 52° 31' 24.2508" N, 13° 24' 41.0400" E New York : 40° 42' 51.3648" N, 74° 0' 21.5064" W . . . Entfernung ¯¯¯¯¯¯¯¯¯¯ d = r · α [rad] = 6385,112
