MatheAss 10.0 − 2-dim. Geometrie
Rechtwinklige Dreiecke
Sind zwei der folgenden Größen gegeben, so berechnet das Programm die anderen.
Gegeben:
¯¯¯¯¯¯¯¯
Hypot.abschnitt p = 1,8
Flächeninhalt A = 6
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
Kathete a = 3
Kathete b = 4
Hypotenuse c = 5
Winkel α = 36,869898°
Winkel β = 53,130102°
Hypot.abschnitt q = 3,2
Höhe h = 2,4
 Dreiecke aus drei Größen
Dreiecke aus drei Größen
Aus drei äußeren Größen ( Seiten oder Winkel ) eines Dreiecks berechnet das Programm die Seiten, die Winkel, die Höhen, die Seiten- und die Winkelhalbierenden, den Umfang und den Flächeninhalt, sowie die Mittelpunkte und Radien von Inkreis und Umkreis des Dreiecks.
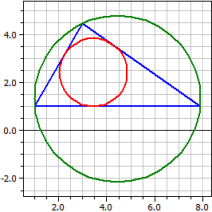
Gegeben: a=6, b=4 und α=60°
Ecken: A(1|1) B(7,899|1) C(3|4,4641)
Seiten: 6 4 6,89898
Winkel: 60° 35,2644° 84,7356°
Höhen: 3,98313 5,97469 3,4641
Seitenh.: 4,77472 6,148 3,75513
Winkelh.: 4,38551 6,11664 3,5464
Umkreis: M(4,44949|1,31784) ru = 3,4641
Inkreis: O(3,44949|2,41421) ri = 1,41421
Fläche: A = 11,9494 Umfang : u = 16,899
 Dreiecke aus drei Punkten
Dreiecke aus drei Punkten
Aus den Koordinaten von drei Eckpunkten berechnet das Programm alle äußeren und inneren Größen (siehe Dreiecke aus drei Größen).
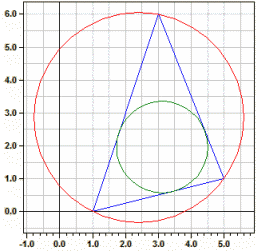
Ecken : A(1|0) B(5|1) C(3|6)
Seiten : 5,38516 6,32456 4,12311
Winkel : 57,5288° 82,2348° 40,2364°
Höhen : 4,0853 3,47851 5,33578
Seitenh. : 4,60977 3,60555 5,5
Winkelh. : 4,37592 3,51849 5,46225
Umkreis : M(2,40909|2,86364) ru = 3,19154
Inkreis : O(3,11866|1,96195) ri = 1,38952
Fläche : A = 11 Umfang : u = 15,8328
 Besondere Geraden und Kreise im Dreieck (Neu in Version 9.0)
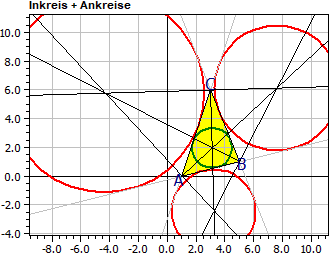
Besondere Geraden und Kreise im Dreieck (Neu in Version 9.0)
Das Programm bestimmt die Gleichungen der Mittelsenkrechten, der Seitenhalbierenden. der Winkelhalbierenden und der Höhen eines Dreiecks. Außerdem die Mittelpunkte und Radien des Umkreises, des Inkreises, der drei Ankreise und des Feuerbachkreises (ab März 2025).
Gegeben:
¯¯¯¯¯¯¯¯
Ecken: A(1|0) B(5|1) C(3|6)
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
Seiten: a : 5·x + 2·y = 27
b : 3·x - y = 3
c : x - 4·y = 1
Inkreis: Mi(3,119|1,962) r i = 1,390
Ankreise: Ma(7,626|6,136) ra = 4,346
Mb(-4,356|5,784) rb = 6,910
Mc(3,248|-2,427) rc = 2,900
 Regelmäßige Vielecke
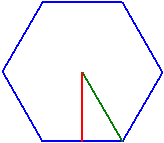
Regelmäßige Vielecke
Sind die Eckenzahl und eine der folgenden Größen gegeben, berechnet das Programm die anderen.
Seite a, Inkreisradius ri , Umkreisradius ru , Umfang u oder Fläche A.

Gegeben:
¯¯¯¯¯¯¯¯
Eckenzahl n = 6
Umfang u = 8
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
Seite a = 1,3333333
Umkreisradius ru = 1,3333333
Inkreisradius ri = 1,1547005
Fläche A = 4,6188022
Beliebige Vielecke (ab November 2022)
Berechnet werden nun auch die Seiten und Winkel des Vielecks und es wird geprüft ob das Vieleck konvex, konkav oder überschlagend ist.
Außerdem werden konvexe Vielecke geprüft, ob sie einen Inkreis und/oder einen Umkreis haben.
Ecken: Fläche A = 16
A(1|2)
B(4,5|0,5) Umfang u = 15,54498
C(6|4)
D(4,5|5,5) Eckenschwerpunkt:
E(1|4) ES(3,4|3,2)
Flächenschwerpunkt:
FS(3,46875|3,07813)
Seiten: Winkel:
|AB| = 3,8078866 ∡BAE = 113,19859°
|BC| = 3,8078866 ∡CBA = 90°
|CD| = 2,1213203 ∡DCB = 111,80141°
|DE| = 3,8078866 ∡EDC = 111,80141°
|EA| = 2 ∡AED = 113,19859°
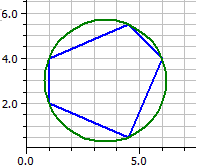
Sehnenvieleck
Umkreis: M(3,5|3) r=2,6925824
Sehnenvieleck:
 Abbildungen
(überarbeitet in Version 9.0)
Abbildungen
(überarbeitet in Version 9.0)
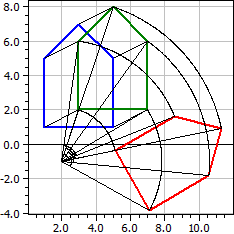
Das Programm erlaubt es, auf ein n-Eck eine Verkettung von Abbildungen anzuwenden. Dabei können Sie wählen aus Verschiebung, Geradenspiegelung, Punktspiegelung, Drehung, Zentrischer Streckung und Scherung.
Urbild A(1|1), B(5|1), C(5|5), D(3|7), E(1|5) Parallelverschiebung: dx=2, dy=1 ☑ A1(3|2), B1(7|2), C1(7|6), D1(5|8), E1(3|6) Drehung: Z(2|-1), α=-60° ☑ A2(5,0981|-0,36603), B2(7,0981|-3,8301), C2(10,562|-1,8301), D2(11,294|0,90192), E2(8,5622|1,634)
 Kreis und Kreisteile
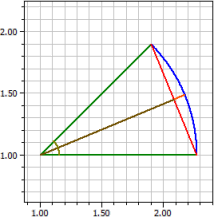
Kreis und Kreisteile
Sind zwei der folgenden Größen gegeben, so berechnet das Programm die anderen.
Gegeben:
¯¯¯¯¯¯¯¯
Bogen b = 1
Winkel α = 45°
Ergebnisse :
¯¯¯¯¯¯¯¯¯¯
Radius r = 1,2732395
Sehne s = 0,97449536
Kreissektor A1 = 0,63661977
Abstand d = 1,17632
Pfeilhöhe h = 0,096919589
Kreissegment A2 = 0,063460604
Kreisfläche A = 5,0929582
Kreisumfang u = 8
 Kreistangenten (Neu in Version 9.0 ab Februar 2021)
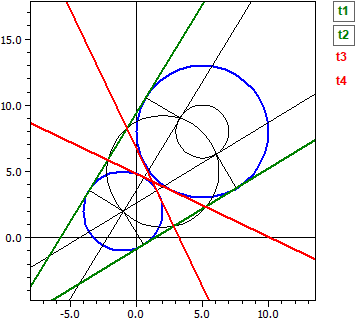
Kreistangenten (Neu in Version 9.0 ab Februar 2021)
Berechnet werden die Gleichungen der folgenden Tangenten:
- Die Tangente an einen Kreis k in einem Punkt B
- Die Tangenten an einen Kreis k durch einen Punkt P außerhalb des Kreises
- Die Tangenten an einen Kreis k parallel zu einer Geraden g
- Die Tangenten an zwei Kreise k1 und k2
Gegeben: ¯¯¯¯¯¯¯¯ k1 : M(5|8) , r =5 k2 : M(-1|2) , r =3 Äußere Tangenten ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ t1: -4,2923·x + 7,04104·y = -6,36427 t2: -7,04104·x + 4,29230·y = 40,3643 Innere Tangenten ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ t3: 1,21895·x + 2,55228·y = 12,3709 t4: -2,55228·x − 1,21895·y = -8,3709
 Ebene Schnitte
Ebene Schnitte
Das Programm berechnet die Schnitte von Geraden und Kreisen
zwei Geraden
g : x + y = 0 h : x - y = 5 Schnittpunkt : S(2,5|-2,5) Schnittwinkel: 90° Abstände zum Ursprung : d(g,O) = 0 d(h,O) = 3,5355339
Gerade und Kreis
k : M(5|0) r = 5 g : x + y = 0 Schnittpunkte : S1(5|-5) S2(0|0)
zwei Kreise
k1 : M1(5|5) r1 = 5 k2 : M2(0|0) r2 = 5 Schnittpunkte : S1(5|0) S2(0|5) Verbindungsgerade : x + y = 5

