MatheAss 10.0 − 3-dim. Geometria
Koordinátarendszerek
Ezzel a programmal a háromdimenziós derékszögű koordináták átszámíthatók gömbi vagy hengerkoordinátákra és vissza.
derékszögű gömbi henger x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Platóni testek
A program kiszámítja az öt platóni testet: tetraéder, hexaéder, oktaéder, dodekaéder és ikozaéder, ha adott az élhossz, a lapmagasság, a testmagasság, a beírt kör sugara, a körülírt kör sugara, a térfogat vagy a felszín.
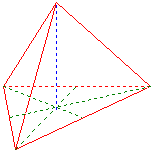
Tetraéder
Adott:
¯¯¯¯¯¯¯¯
Körülírt kör sugara ru = 1
Eredmények:
¯¯¯¯¯¯¯¯¯¯
Él a = 1,6329932
Lapmagasság h1 = 1,4142136
Testmagasság h2 = 1,3333333
Beírt kör sugara ri = 0,33333333
Térfogat V = 0,51320024
Felszín O = 4,6188022
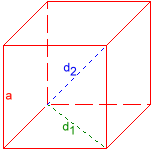
Hexaéder
Adott:
¯¯¯¯¯¯¯¯
Felszín O = 8
Eredmények:
¯¯¯¯¯¯¯¯¯¯
Él a = 1,1547005
Lapátló d1 = 1,6329932
Testátló d2 = 2
Körülírt kör sugara ru = 1
Beírt kör sugara ri = 0,57735027
Térfogat V = 1,5396007
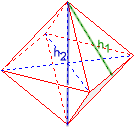
Oktaéder
Adott:
¯¯¯¯¯¯¯¯
Térfogat V = 4/3
Eredmények:
¯¯¯¯¯¯¯¯¯¯
Él a = 1,4142136
Lapmagasság h1 = 1,2247449
Testmagasság h2 = 2
Körülírt kör sugara ru = 1
Beírt kör sugara ri = 0,57735027
Felszín O = 6,9282032
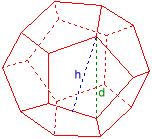
Dodekaéder
Adott:
¯¯¯¯¯¯¯¯
Lapátló d = 2
Eredmények:
¯¯¯¯¯¯¯¯¯
Él a = 1,236068
Lapmagasság h = 1,902113
Körülírt kör sugara ru = 1,7320508
Beírt kör sugara ri = 1,3763819
Térfogat V = 14,472136
Felszín O = 31,543867
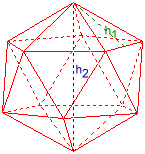
Ikosaéder
Adott:
¯¯¯¯¯¯¯¯
Testmagasság h2 = 2
Eredmények:
¯¯¯¯¯¯¯¯¯
Él a = 1,0514622
Lapmagasság h1 = 0,910593
Körülírt kör sugara ru = 1
Beírt kör sugara ri = 0,79465447
Térfogat V = 2,5361507
Felszín O = 9,5745414
Egyéb testek
A program kiszámítja egy szabályos prizma, egy álló körhenger, egy négyzetes gúla, egy álló körkúp vagy egy gömb minden adatát, ha kettő közülük adott.
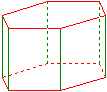
A prizma
Adott: n = 4
¯¯¯¯¯¯¯¯
Térfogat V = 1
Felszín O = 6
Eredmények:
¯¯¯¯¯¯¯¯¯
Oldal a = 1
Magasság h = 1
Körülírt kör sugara ru = 0,70710678
Beírt kör sugara ri = 0,5
Alapterület G = 1
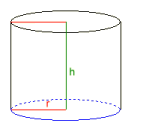
A körhenger
Adott:
¯¯¯¯¯¯¯¯
Sugár r = 1
Térfogat V = 1
Eredmények:
¯¯¯¯¯¯¯¯¯¯
Magasság h = 0,31830989
Kerület u = 6,2831853
Alapterület G = 3,1415927
Palástfelület M = 2
Felszín O = 8,2831853
A körhenger
Adott:
¯¯¯¯¯¯¯¯
Sugár r = 1
Térfogat V = 1
Eredmények:
¯¯¯¯¯¯¯¯¯¯
Magasság h = 0,31830989
Kerület u = 6,2831853
Alapterület G = 3,1415927
Palástfelület M = 2
Felszín O = 8,2831853
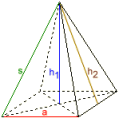
A négyzetes gúla
Adott:
¯¯¯¯¯¯¯¯
Alapél a = 1
Térfogat V = 1
Eredmények:
¯¯¯¯¯¯¯¯¯
Oldalél s = 3,082207
Testmagasság h1 = 3
Oldalmagasság h2 = 3,0413813
Felszín O = 7,0827625
Oldalfelület A = 1,5206906
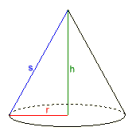
A körkúp
Adott:
¯¯¯¯¯¯¯¯
Térfogat V = 1
Alapterület G = 1
Eredmények:
¯¯¯¯¯¯¯¯¯¯
Sugár r = 0,56418958
Magasság h = 3
Alkotó s = 3,0525907
Palástfelület M = 5,4105761
Felszín O = 6,4105761
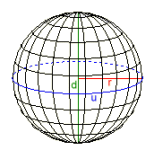
A gömb
Adott:
¯¯¯¯¯¯¯¯
Felszín O = 1
Eredmények:
¯¯¯¯¯¯¯¯¯¯
Sugár r = 0,28209479
Átmérő d = 0,56418958
Kerület u = 1,7724539
Térfogat V = 0,094031597
Egyenes 2 ponton át
Egyenes A(1|1|1), B(2|5|6)
Paraméteres alak
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
x = ⎪ 1 ⎪ + t·⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 5 ⎭
Távolság az origótól
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 0,78679579
Helyzet az xy-síkhoz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
merőleges vetület: 4·x - y = 3
Metszéspont: S1(0,8|0,2|0)
Metszési szög: 50,490288°
Helyzet a yz-síkhoz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
merőleges vetület: 5·x - 4·y = 1
Metszéspont: S2(0|-3|-4)
Metszési szög: 8,8763951°
Helyzet az xz-síkhoz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
merőleges vetület: 5·x - y = 4
Metszéspont: S3(0,75|0|-0,25)
Metszési szög: 38,112927°
Sík 3 ponton át
Sík a pontokon át:
A(1|2|3), B(2|3|3), C(1|0|1)
Pont-iránymértékes alak:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
Koordinátaegyenlet:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Távolság az origótól:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Nyompontok:
¯¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)
Gömb 4 ponton át
Gömb a pontokon át: A(1|0|0), B(0|2|0), C(0|0|3), D(1|0|1) Normálalak: ¯¯¯¯¯¯¯¯¯¯¯ | -> ⎧-2,5 ⎫ |2 K: | x - ⎪-0,5 ⎪ | = 12,75 | ⎩ 0,5 ⎭ | Középpont és sugár: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ M(-2,5|-0,5|0,5) r = 3,5707142
Metszések a térben
A program kiszámítja egyenesek, síkok és gömbök metszéspontjait.
két egyenes
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Metszéspont : S(5|5|5)
Metszési szög: 60°
Távolságok az origótól :
d(O,g)=5 d(O,h)=5
Sík és egyenes
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
E : x + y + z = 5
Metszéspont : S(5|0|0)
Metszési szög: 54,73561°
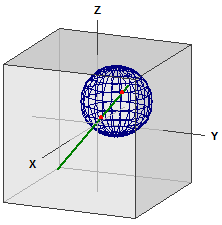
Gömb és egyenes
-> ⎧ 1 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
K : M(5|5|5) , r = 5
Metszéspontok :
S1(2,8187|1,8187|1,8187)
S2(8,5147|7,5147|7,5147)
A húr hossza :
s = 9,8657657
két sík
Adott síkok:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1 : 5·x - 2·y = 5
E2 : 2·x - y + 5·z = 8
A síkok metszőegyenese:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> |-11 | | 10 |
g : x = |-30 | + r·| 25 |
| 0 | | 1 |
Távolság az origótól:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,5057283
A síkok metszési szöge:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 65,993637°
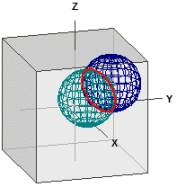
két gömb
Adott gömbök: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ K1 : M1(3|3|3) , r1 = 3 K2 : M2(1|1|1) , r2 = 3 Metszőkör: ¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2), r = 2,4494897 Metszősík: ¯¯¯¯¯¯¯¯¯¯¯¯¯ E : x + y + z = 6
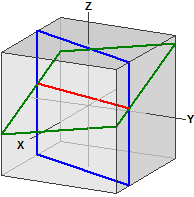
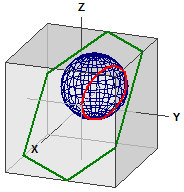
Gömb és sík
Sík :
¯¯¯¯¯¯¯
E : 5·x - 4·y + 5·z = -3
Gömb :
¯¯¯¯¯¯¯
| -> ⎧ 1 ⎫|2
K : | x - ⎪ 2 ⎪| = 16
| ⎩ 3 ⎭|
A K és E metszőkörének adatai :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-0,13636|2,9091|1,8636)
r = 3,548367
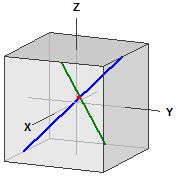
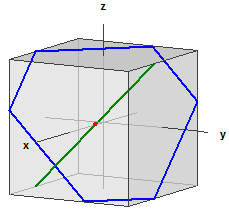
Távolságok a gömbön
(Új a 9.0 verzióban, 2021 decemberétől)
A program kiszámítja két pont távolságát egy gömbön. Ehhez a MatheAss több funkcióját összesíti.
GPS decimális ¯¯¯¯¯¯¯¯¯¯¯ Berlin : 52.523403, 13.4114 New York : 40.714268, -74.005974 GPS fok-perc-másodperc ¯¯¯¯¯¯¯ Berlin : 52° 31' 24.2508" É, 13° 24' 41.0400" K New York : 40° 42' 51.3648" É, 74° 0' 21.5064" Ny . . . Távolság ¯¯¯¯¯¯¯¯¯¯ d = r · α [rad] = 6385,112
