MatheAss 10.0 − Algebra

Prímszámok

A program kiszámítja az összes prímszámot két szám között.

Prímszámok 1000000000 és 1000000300 között:

1000000007 1000000009 1000000021 1000000033 1000000087 1000000093
1000000097 1000000103 1000000123 1000000181 1000000207 1000000223
1000000241 1000000271 1000000289 1000000297

16 prímszám

Prímszám párok (Új a 9.0 verzióban)

A program meghatározza az [a,b] intervallumban az összes ikerprímet (p,p+2), unokatestvér prímeket (p,p+4), „szexi” prímeket (p,p+6) és hármas prímszámokat.

Prímszám hármasok 1 és 200 között

(3|5|7) (5|7|11) [7|11|13] (11|13|17) [13|17|19] (17|19|23) [37|41|43] 
(41|43|47) [67|71|73] [97|101|103] (101|103|107) [103|107|109] (107|109|113)
(191|193|197) [193|197|199] 

15 hármas prímszám
7 a (p|p+2|p+6) alakban és 7 a [p|p+4|p+6] alakban

Prímtényezős felbontás

A program felbontja a természetes számokat prímtényezőkre.

  99999999999901 = 19001 · 5262880901
  99999999999001 = 107 · 401 · 1327 · 1756309
  99999999990001 = prímszám 
    3938980639167 = 3¹⁴ · 7⁷
999330136292431 = 99971² · 99991

LNKO és LKKT

Két szám a és b esetén meghatározza a legnagyobb közös osztót, a legkisebb közös többszörost és az osztóhalmazokat.

a = 24
b = 256

legnagyobb közös osztó          LNKO = 8
legkisebb közös többszörös    LKKT = 768  

Osztóhalmazok :
T(a) = { 1 2 3 4 6 8 12 24}
T(b) = { 1 2 4 8 16 32 64 128 256}

Százalékszámítás (Új a 9.0 verzióban)

Kiszámítja az alapértéket G, a százalékértéket W, a százalékos arányt p ill. p%, a növekedési tényezőt q és a végértéket E, ha ezek közül kettőt megadunk.

Adott:
¯¯¯¯¯¯¯¯
        Százalékérték  W = −120
Növekedési tényező  q = 95% = 0,95 = 19/20

Eredmények:
¯¯¯¯¯¯¯¯¯¯
                Alapérték  G = 2400
Százalékos arány  p% = −5% = −0,05 = −1/20      
                 Végérték  E = 2280

Tizedes számok törtekben

A program átalakítja a periodikus és véges tizedestörteket közönséges törtekké.

Nem periodikus rész : 1.20
Periódus : 045
    ___
1.20045 = 120/100 + 1/2220 = 533/444

Törtek tizedes számokban

A program átalakítja a törteket periodikus tizedestörtekké, és meghatározza a periódust és annak hosszát.

Számláló : 533
Nevező : 444
              ___
533/444 = 1.20045
periodikus a 3. tizedesjegytől
a periódus 3 számjegy hosszú

Binomiális képletek

Az iskolai matematika legismertebb képletei közé tartozik a binomiális képlet (a + b)² = a² + 2ab + b² .

A program kiszámítja az általánosabb esetet (a·x + b·y)ⁿ.

(2·x  − 3·y)⁷ =       +128 · x⁷
                           −1344 · x⁶ · y
                            +6048 · x⁵ · y²
                          −15120 · x⁴ · y³   
                          +22680 · x³ · y⁴
                          −20412 · x² · y⁵
                          +10206 · x · y⁶
                            −2187 · y⁷

A program meghatározza egy 4. vagy kisebb fokú egyenlet valós értékű megoldásait. Magasabb fokú egyenletek esetén – a közelítő számításokon (nullhelyek a függvényvizsgálatban) kívül – nincs algebrai megoldási eljárás.

x⁴ + 2·x³ - 3·x² + 5·x - 5 = 0   <=>   (x - 1)·(x³ + 3·x² + 5) = 0
L = {-3,42599;  1}

Diophantoszi egyenletek

Nevét az alexandriai Diophantoszról kapta (kb. 250), aki Arithmetica című könyvében a lineáris és másodfokú egyenletek megoldását, különösen azok egész megoldásait tárgyalta.
A program kiszámítja az egész megoldásokat az a·x - b·y - c = 0 egyenletre. Így meghatározhatók az egész koordinátájú pontok egy egyenesen.

7·x − 3·y − 5 = 0 ;   x,y egész szám
L = { ( 2 + 3t | 3 + 7t ) }

Püthagoraszi számhármasok

A püthagoraszi számhármasok az (x,y,z) egész megoldások az x² + y² = z² egyenletre, amely derékszögű háromszögek oldalaira vonatkozik.

x, y, z értékek 100 és 400 között:

( 119, 120, 169 )    ( 104, 153, 185 )    ( 133, 156, 205 )    ( 105, 208, 233 )    
( 140, 171, 221 )    ( 115, 252, 277 )    ( 120, 209, 241 )    ( 161, 240, 289 )    
( 160, 231, 281 )    ( 207, 224, 305 )    ( 175, 288, 337 )    ( 135, 352, 377 )    
( 136, 273, 305 )    ( 204, 253, 325 )    ( 225, 272, 353 )    ( 189, 340, 389 )    
( 180, 299, 349 )    ( 252, 275, 373 )    ( 152, 345, 377 )    ( 228, 325, 397 )

Számologépek

Négy számologép áll rendelkezésre:

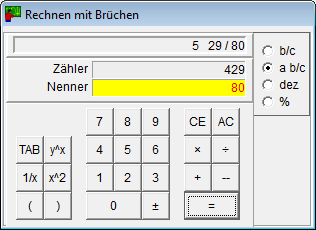
A törtszámologép kezeli a négy alapműveletet és hatványozni is tud.
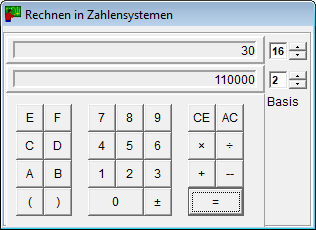
A számrendszer-számologép bármely alapot használ 2 és 16 között.
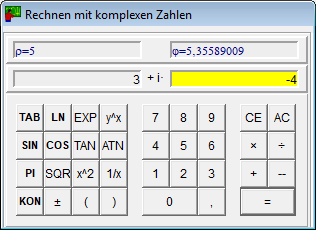
A komplex számok számologépe a szokásos műveleteken kívül kiszámítja egy szám komplex konjugáltját is.
A nagy egész számok számologépe kezeli az alapműveleteket és a kombinatorikai képleteket.

Számolás nagy számokkal (Új a 9.0 verzióban, 2021 áprilisától)

Számolás legfeljebb 10 000 jegyű egész számokkal.

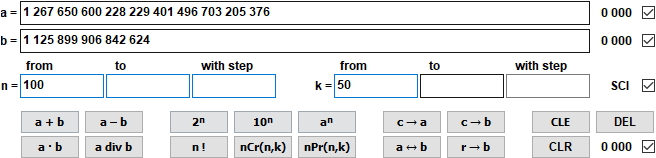
1 267 650 600 228 229 401 496 703 205 376   div  1 125 899 906 842 624  
 =  1 125 899 906 842 624  maradék  0
 =  1,13 · 10^15 maradék 0

nCr(100,50)  =  100 891 344 545 564 193 334 812 497 256 = 1,01 · 10^29