MatheAss 10.0 − Lineáris algebra

Lineáris egyenletrendszerek

A program meghatározza egy n egyenletből és n ismeretlenből álló lineáris egyenletrendszer megoldásvektorát.

Példa: Ha parabolát keresünk a P(1/3), Q(2/1) és R(4/9) pontokon át, akkor az alábbi egyenletrendszert kapjuk:

  1·x1 + 1·x2 + 1·x3 = 3
  4·x1 + 2·x2 + 1·x3 = 1
 16·x1 + 4·x2 + 1·x3 = 9   
            
 L = ( 2; -8; 9 )

A parabola egyenlete tehát: y = 2x² - 8x + 9.

Példa kétdimenziós megoldástérrel:

  0·x1 + 0·x2 + 2·x3 - 1·x4  =  1
  1·x1 + 1·x2 + 1·x3 + 1·x4  =  4
  2·x1 + 2·x2 - 4·x3 + 5·x4  =  5
  1·x1 + 1·x2 - 7·x3 + 5·x4  =  0

  L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }

Lineáris optimalizálás (2022 februárjától)

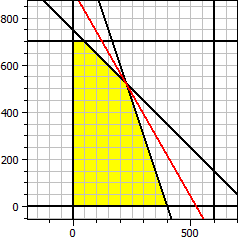
A program meghatározza egy kétváltozós célfüggvény optimális megoldását lineáris egyenlőtlenségek által adott feltételek mellett.

Célfüggvény:   
  ƒ(x,y) = 140·x + 80·y → Maximum

Feltételek:
  x ≥ 0
  y ≥ 0
  x ≤ 600
  y ≤ 700
  x + y ≤ 750
  3·x + y ≤ 1200

Maximum
  x = 225   y = 525
  ƒ(x,y) = 73500

A program meghatározza egy vektor lineáris kombinációját három adott vektorból. A rutin alkalmas annak vizsgálatára is, hogy három vektor lineárisan független-e a térben, azaz egy síkban helyezkednek-e el.

    ⎧ 1 ⎫     ⎧ 2 ⎫     ⎧ 0 ⎫   ⎧ 2 ⎫
  a·⎪ 2 ⎪ + b·⎪ 1 ⎪ + c·⎪ 1 ⎪ = ⎪ 3 ⎪   
    ⎩ 0 ⎭     ⎩ 1 ⎭     ⎩ 0 ⎭   ⎩ 7 ⎭

Megoldás :
  a = -12  b = 7  c = 20

Skalárszorzat

A program kiszámítja két vektor skalárszorzatát, a vektorok hosszát és a közöttük lévő szöget.

   ->  ⎧ 1 ⎫   ->  ⎧ 5 ⎫
   a = ⎪ 3 ⎪   b = ⎪ 0 ⎪
       ⎩ 1 ⎭       ⎩ 3 ⎭

A vektorok skalárszorzata = 8

Az első vektor hossza   = √11 = 3,3166248
A második vektor hossza = √34 = 5,8309519

A közbezárt szög  α = 65,564402°

Vektorszorzat

A program kiszámítja két vektor vektorszorzatát, valamint annak abszolút értékét. A vektorszorzat merőleges az általuk kifeszített paralelogrammára, és nagysága megegyezik a paralelogramma területével.

     ->  ⎧ 1 ⎫     ->  ⎧ 7 ⎫
     a = ⎪ 2 ⎪     b = ⎪ 1 ⎪
         ⎩ 3 ⎭         ⎩ 4 ⎭

 ->  ->  ⎧  5 ⎫    ->  ->  
 a x b = ⎪ 17 ⎪   |a x b|= √483 = 21,977261
         ⎩-13 ⎭

Térszorzat

A program kiszámítja három vektor térszorzatát. Ennek abszolút értéke megadja az általuk kifeszített eltolódott hasáb (paralelopipedon) térfogatát.

  ->  ⎧ 2 ⎫     ->  ⎧ 2 ⎫     ->  ⎧ 3 ⎫   
  a = ⎪ 3 ⎪     b = ⎪-1 ⎪     c = ⎪ 9 ⎪
      ⎩ 5 ⎭         ⎩ 7 ⎭         ⎩ 2 ⎭

    ->  ->    ->  
  ( a x b ) · c = 26

Mátrixinverzió

A program kiszámítja egy n-ed rendű négyzetes mátrix determinánsát, rangját és inverzét.

Mátrix: 

  ⎧  0  1  1  ⎫
  ⎪  0  1  3  ⎪
  ⎩  2  0  1  ⎭

Inverz mátrix

  ⎧  0,25 -0,25  0,5  ⎫
  ⎪   1,5  -0,5    0  ⎪
  ⎩  -0,5   0,5    0  ⎭

Rend = 3,  Rang = 3,  Determináns = 4

Pszeudoinverz mátrix

Ha egy mátrix A oszlopai lineárisan függetlenek, akkor A^T· A invertálható, és a pszeudoinverz a következő képlettel számítható:

A⁺ = ( A^T· A )^-1· A^T

Ekkor A⁺ az A bal inverze, azaz teljesül: A⁺ · A = E .

Mátrix A
¯¯¯¯¯¯¯¯
  ⎧  1  1  1  1  ⎫
  ⎩  5  7  7  9  ⎭

A^T· A
¯¯¯¯
  ⎧  26  36  36  46  ⎫
  ⎪  36  50  50  64  ⎪
  ⎪  36  50  50  64  ⎪
  ⎩  46  64  64  82  ⎭

A^T· A nem invertálható

A · A^T
¯¯¯¯
  ⎧   4   28  ⎫
  ⎩  28  204  ⎭

( A · A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧  6,375 -0,875  ⎫
  ⎩ -0,875  0,125  ⎭

Jobbinverz:  A^T · ( A · A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧     2  -0,25  ⎫
  ⎪  0,25      0  ⎪
  ⎪  0,25      0  ⎪
  ⎩  -1,5   0,25  ⎭

Mátrixszorzás

A program kiszámítja két mátrix szorzatát.

 1. Mátrix           2. Mátrix

  ⎧  1  2  3  0  ⎫   ⎧  1   2   3   4  ⎫
  ⎪  4  5  6  0  ⎪   ⎪  5   6   7   8  ⎪
  ⎪  0  0  0  0  ⎪   ⎪  9  10  11  12  ⎪
  ⎩  0  0  0  0  ⎭   ⎩  0   0   0   0  ⎭

 Szorzatmátrix
  
  ⎧  38  44   50   56  ⎫
  ⎪  83  98  113  128  ⎪
  ⎪   0   0   0    0   ⎪
  ⎩   0   0   0    0   ⎭

MatheAss 10.0 − Lineáris algebra

A+ = ( AT· A )-1· AT

A⁺ = ( A^T· A )^-1· A^T