MatheAss 10.0 − Analízis

Sorozatok és sorok   (Új a 9.0 verzióban, 2021 májusától)

A program meghatározza egy sorozat  (ai)  első n elemét és a hozzátartozó sort (a sorozatelemek összegét), ha a sorozat első elemei és egy explicit függvény  ai=ƒ(i)  vagy egy rekurziós képlet  ai=ƒ(a0, a1, ... , ai-1)  adottak.

a[0]=1;   a[1]=1;   a[ i ] = a[i-1] + a[i-2];   n = 20

Sorozat
¯¯¯¯¯
( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765)

Sor
¯¯¯¯¯
( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)

Polinomok osztása

A program kiszámítja két polinom szorzatát és hányadosát.

1. Polinom:  3·x4 - 2·x + 1
2. Polinom:  2·x + 5

      Szorzat:  6·x5 + 15·x4 - 4·x2 - 8·x + 5                 
     Hányados:  3/2·x3 - 15/4·x2 + 75/8·x - 391/16
           Maradék:  1971/16

Polinomok faktorizálása   (Új a 9.0 verzióban)

A program kiszámítja egy polinom racionális gyökeit és lineáris tényezőkre bontását.

p(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 + x - 9
       = (1/9)·(9·x5 - 81·x4 - 82·x3 + 738·x2 + 9·x - 81)
       = (1/9)·(3·x - 1)·(3·x + 1)·(x - 9)·(x - 3)·(x + 3)

Racionális gyökök: 1/3, -1/3, 9, 3, -3

Polinomok transzformálása   (Új a 9.0 verzióban)

Egy polinomfüggvény  ƒ(x)  eltolható vagy nyújtható x- és y-iránnyal.

ƒ(x) =  - 1/4·x4 + 2·x3 - 16·x + 21

Eltolás dx = -2 ,  dy = 0                             

ƒ(x + 2) =  - 1/4·x4 + 6·x2 + 1

Polinomok lnko és lkkt  (Új a 9.0 verzióban, 2021 februárjától)

A program kiszámítja két polinom legnagyobb közös osztóját (lnko) és legkisebb közös többszörösét (lkkt).

p1(x) =  4·x6 - 2·x5 - 6·x4- 18·x3 - 2·x2 + 24·x + 8
p2(x) =  10·x4- 14·x3 - 22·x2 + 14·x + 12

lnko(p1,p2) =  x2 - x - 2
lkkt(p1,p2) =  40·x8 - 36·x7 - 76·x6 - 144·x5 + 88·x4+ 356·x3 - 4·x2 - 176·x - 48

Függvényábrázoló 1

Legfeljebb tíz függvény rajzolható meg egyszerre egy koordinátarendszerben. Megengedettek a már definiált függvények összekapcsolásai vagy deriváltjai is.

Legyen  ƒ1(x)=sin(x) és ƒ2(x)=3*sqrt(x), ekkor

ƒ3(x)=2*y1^2-y2         ƒ3(x)=2*sin(x)^2-3*sqrt(x)
ƒ4(x)=f2(y1)               ƒ4(x)=3*sqrt(sin(x))
ƒ5(x)=y2'                   ƒ5(x)=3/(2*sqrt(x))

Példa: ƒ1(x)=sin(x),   ƒ2(x)=x   és   ƒ3(x)=y1+y2

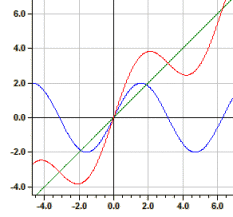
Függvényábrázoló 2

Egy szakaszonként definiált függvény kerül megrajzolásra, amelyet kilenc részfüggvény ad meg. Minden részfüggvényhez meg kell adni a definíciós tartományt, az intervallum típusát és a színt. Ezenkívül meghatározható, hogy a határpontok megrajzolásra kerüljenek-e vagy sem.

Példa:

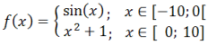
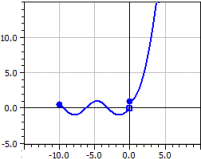
Paramétergörbék

Ezzel a programmal olyan görbéket lehet rajzolni, amelyek nem egy explicit függvényalak által adottak, hanem két függvény írja le a vízszintes és függőleges kitérést.

Példa: Lissajous-figurák

    x(k) = sin(3*k)

    y(k) = cos(5*k)

    k -Pi-től Pi-ig

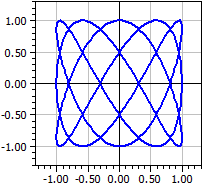
Lissajous-figurákat kapunk, ha egy oszcilloszkópra két különböző frekvenciájú váltakozó feszültséget kapcsolunk.

Görbeseregek

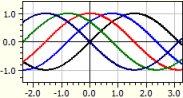
A program megrajzolja tetszőleges függvények grafikonját, amelyek egy k paramétert tartalmaznak. A  k  értékei felsorolhatók, vagy kezdőérték, végérték és lépésköz megadásával határozhatók meg.

    ƒ(x,k) = sin(x+k)

    k -2-től 2-ig, lépésköz Pi/4

Polinomfüggvények   (Új a 9.0 verzióban)

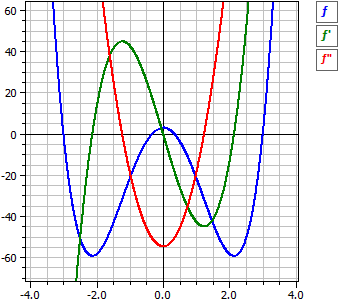
A program egy egészracionális függvény (polinomfüggvény) esetén elvégzi a függvényvizsgálatot. Ez azt jelenti, hogy meghatározza a deriváltakat és a primitív függvényt (ősfunkciót), valamint megvizsgálja a függvényt racionális gyökök, szélsőértékek, inflexiós pontok és szimmetria szempontjából. 

Függvény :
¯¯¯¯¯¯¯¯
ƒ(x) = 3·x4 - 82/3·x2 + 3
       = 1/3·(9·x4 - 82·x2 + 9)
       = 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)                  

Deriváltak :
¯¯¯¯¯¯¯¯¯¯
ƒ'(x)  = 12·x3 - 164/3·x
ƒ"(x)  = 36·x2 - 164/3
ƒ'"(x) = 72·x

Ősfunkció
¯¯¯¯¯¯¯¯¯¯¯¯
ƒ(x) = 3/5·x5 - 82/9·x3 + 3·x + c

  .
  .
  .

Racionális függvények   (Új a 9.0 verzióban)

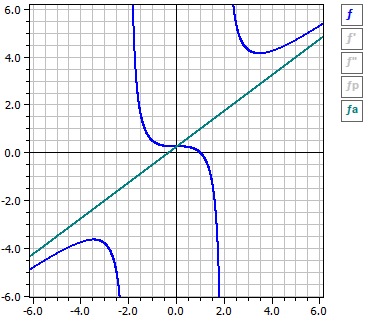
A program egy (tört)racionális függvény esetén elvégzi a függvényvizsgálatot. Ez azt jelenti, hogy meghatározza a deriváltakat, a definíciós hézagokat és a folytonos kiterjesztést. A függvényt megvizsgálja zérushelyek, szélsőértékek, inflexiós pontok és a |x|→ ∞ esetén mutatott viselkedés szempontjából. 

Függvény :
¯¯¯¯¯¯¯¯
            3·x3 + x2 - 4         (x - 1)·(3·x2 + 4·x + 4)  
ƒ(x) = —————— = ———————————
               4·x2 - 16                4·(x - 2)·(x + 2)       

Definíciós hézagok
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x = 2  pólus előjelváltással
x = -2 pólus előjelváltással

Deriváltak :
¯¯¯¯¯¯¯¯¯¯
               3·(x4 - 12·x2)             3·(x2·(x2 - 12))   
ƒ'(x) = ———————— = —————————
            4·(x4 - 8·x2 + 16)       4·(x - 2)2·(x + 2)2 

                     6·(x3 + 12·x)                6·(x·(x2 + 12))  
ƒ"(x) = ——————————— = ————————
             x6 - 12·x4 + 48·x2 - 64        (x - 2)3·(x + 2)3 

  .
  .
  .

Függvényvizsgálat

A program tetszőleges függvény esetén elvégzi a függvényvizsgálatot. Ez azt jelenti, hogy meghatározza a deriváltakat, megvizsgálja a függvényt zérushelyek, szélsőértékek és inflexiós pontok szempontjából, megrajzolja ƒ, ƒ' és ƒ" grafikonját, valamint kiad egy értéktáblázatot. 

Függvény :
‾‾‾‾‾‾‾‾‾‾‾‾‾
  ƒ(x) = x^4 - 2*x^3 + 1
  Vizsgálat a -10 és 10 közötti tartományban                

Deriváltak:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  ƒ'(x) = 4*x^3-6*x^2
  ƒ"(x) = 12*x^2-12*x

Zérushelyek:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  N1( 1 | 0 )                  m = -2
  N2( 1,83929 | 0 )       m =  4,5912

Szélsőértékek:
‾‾‾‾‾‾‾‾‾‾‾‾
  T1( 1,5 |-0,6875 )      m = 0

Inflexiós pontok:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  W1( 0 | 1 )                 m = 0
  W2( 1 | 0 )                 m = -2

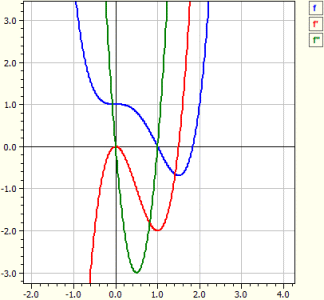
Newton-iteráció

A Newton-iteráció egy közelítő eljárás egy függvény zérushelyének meghatározására. Ha megadunk egy x0 kezdőértéket, amely elég közel van a keresett zérushelyhez, akkor a következő közelítés a ƒ grafikonjához húzott érintő és az x-tengely metszéspontja lesz a P(x0 / ƒ(x0)) pontban. 

  ƒ(x) = x-cos(x)

                 x                       ƒ(x)                  ƒ'(x) 
   ————————   ——————   ——————   
   x0 = 1
   x1 = 0,75036387     0,45969769       1,841471
   x2 = 0,73911289     0,018923074     1,681905
   x3 = 0,73908513     0,00004646       1,6736325
   x4 = 0,73908513     0,00000000       1,673612

Integrálszámítás   (2021 februárjától ívhosszal)

Kiszámítja két függvénygörbe közötti terület orientált és abszolút értékét egy megadott intervallumban. Ezenkívül meghatározza:
- a nyomatékokat az x- illetve y-tengely körüli forgatásnál,
- az így létrejövő forgástestek térfogatát,
- az ívhosszakat az [a;b] intervallumban és
- a terület súlypontját (ha A1=A2).

  ƒ1(x) = cosh(x)
  ƒ2(x) = x^2+1

  Integrációs intervallum  [a;b]  -2-től 2-ig

  Orientált terület :  A1 = -2,07961
  Abszolút terület  :  A2 = 2,07961

  Ívhosszak         :  L1[a;b] = 7,254    L2[a,b] = 9,294

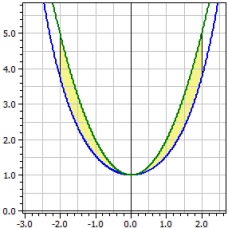
Sorfejtés

Megrajzolásra kerül egy sorral adott függvény, ahol a sorfejtések különböző paramétertartományokra összehasonlíthatók, és a jobb megkülönböztetés érdekében y-iránnyal eltolhatók. 

A Taylor-sor első 16 tagja 
a szinuszfüggvényre.

ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) ,   
k = 4, 8 és 16

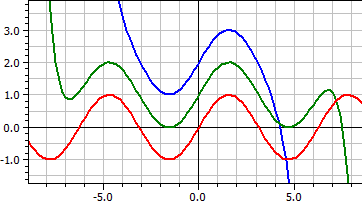
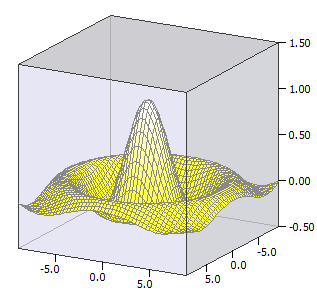
Felületfüggvények

Megrajzolásra kerül egy felületfüggvény ƒ(x,y), vagyis egy kétváltozós függvény háromdimenziós ábrája.

Példa:

ƒ(x, y) = sin(u) / u    
u(x, y) = sqrt(x * x + y * y)

   -9 ≤ x ≤ 9
   -9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5