MatheAss 10.0 − 2-dim. Geometria

Derékszögű háromszögek

Ha a következő méretek közül kettő adott, a program kiszámítja a többit. 

Adott:
¯¯¯¯¯¯¯¯
  Hipot. szakasz  p = 1,8
        Terület  A = 6 
 
Eredmények:
¯¯¯¯¯¯¯¯¯¯
              Befogó  a = 3
              Befogó  b = 4
        Átfogó  c = 5
               Szög  α = 36,869898°
               Szög  β = 53,130102°  
 Hipot. szakasz  q = 3,2
                 Magasság  h = 2,4

Háromszögek három adatból

Három külső adatból (oldalak vagy szögek) a program kiszámítja az oldalakat, a szögeket, a magasságokat, az oldal- és szögfelezőket, a kerületet és a területet, valamint a belső és külső kör középpontját és sugarát. 

Adott: a=6, b=4 és α=60°

      Csúcsok:   A(1|1)         B(7,899|1)   C(3|4,4641)
      Oldalak:   6                4                  6,89898
     Szögek:   60°             35,2644°     84,7356° 
     Magasságok:   3,98313      5,97469      3,4641 
  Oldalf.:   4,77472      6,148          3,75513
  Szögf.:   4,38551      6,11664      3,5464

  Körülírt kör:   M(4,44949|1,31784)       ru = 3,4641
  Beírt kör:   O(3,44949|2,41421)        ri = 1,41421

    Terület: A = 11,9494      Kerület : u = 16,899
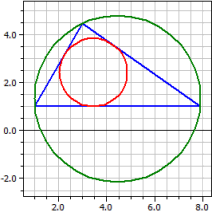
Háromszög 2

Háromszögek három pontból

Három csúcs koordinátáiból a program kiszámítja az összes külső és belső adatot (lásd Háromszögek három adatból). 

      Csúcsok : A(1|0)          B(5|1)          C(3|6) 
     Oldalak : 5,38516       6,32456       4,12311
     Szögek : 57,5288°     82,2348°     40,2364° 
     Magasságok : 4,0853        3,47851       5,33578
  Oldalf. : 4,60977       3,60555       5,5 
 Szögf. : 4,37592       3,51849       5,46225

 Körülírt kör : M(2,40909|2,86364)     ru = 3,19154
 Beírt kör :  O(3,11866|1,96195)      ri = 1,38952  
   
 Terület :  A = 11            Kerület : u = 15,8328
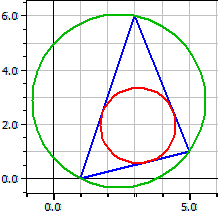
Háromszög 3

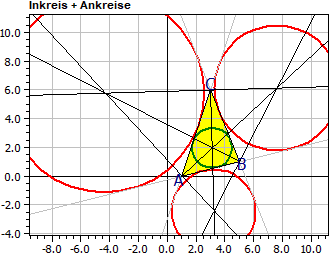
Különleges egyenesek és körök a háromszögben   (Új a 9.0 verzióban)

A program meghatározza a háromszög oldalfelező merőlegeseit, oldalfelezőit, szögfelezőit és magasságait. Továbbá a körülírt kör, a beírt kör, a három érintőkör és a Feuerbach-kör középpontját és sugarát (2025 márciustól).

Adott:
¯¯¯¯¯¯¯¯
       Csúcsok:    A(1|0)   B(5|1)   C(3|6)
 
Eredmények:
¯¯¯¯¯¯¯¯¯¯
      Egyenesek:   a :  5·x + 2·y = 27
                    b :  3·x - y = 3
                    c :  x - 4·y = 1
 
     Beírt kör:    Mi(3,119|1,962)         r i = 1,390
 
  Érintőkörök:    Ma(7,626|6,136)       ra = 4,346
                     Mb(-4,356|5,784)      rb = 6,910
                     Mc(3,248|-2,427)      rc = 2,900

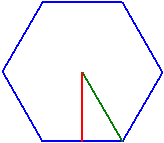
Szabályos sokszögek

Ha adott a csúcsszám és a következő adatok közül egy, a program kiszámítja a többit.
Oldal a, beírt kör sugara ri , körülírt kör sugara ru , kerület u vagy terület A.

Adott:
¯¯¯¯¯¯¯¯
      Csúcsszám  n = 6
          Kerület  u = 8      
 
Eredmények:
¯¯¯¯¯¯¯¯
              Oldal  a = 1,3333333
Körülírt kör sugara ru = 1,3333333
   Beírt kör sugara ri = 1,1547005
            Terület  A = 4,6188022                        

Tetszőleges sokszögek   (2022 novemberétől)

A program kiszámítja a sokszög oldalait és szögeit, valamint ellenőrzi, hogy a sokszög konvex, konkáv vagy önátmetsző.
Továbbá a konvex sokszögeknél megvizsgálja, hogy van-e beírt és/vagy körülírt körük.

Csúcsok:                         Terület  A = 16
 A(1|2)                          
 B(4,5|0,5)                     Kerület  u = 15,54498
 C(6|4)                           
 D(4,5|5,5)                     Csúcstömegközéppont: 
 E(1|4)                           ES(3,4|3,2)

                                 Súlypont: 
                                 FS(3,46875|3,07813)

Oldalak:                         Szögek:
 |AB| = 3,8078866          ∡BAE = 113,19859°
 |BC| = 3,8078866          ∡CBA = 90°
 |CD| = 2,1213203          ∡DCB = 111,80141°
 |DE| = 3,8078866          ∡EDC = 111,80141°
 |EA| = 2                   ∡AED = 113,19859°

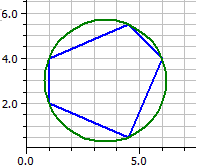
Húr-sokszög
Körülírt kör:  M(3,5|3)  r=2,6925824

Húr-sokszög:

Leképezések   (felülvizsgálva a 9.0 verzióban)

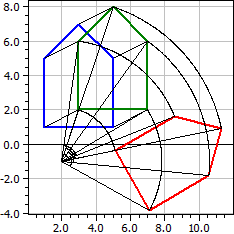
A program lehetővé teszi, hogy egy n-szögre leképezések sorozatát alkalmazzuk. Választható: eltolás, egyenestükrözés, ponttükrözés, forgatás, középpontos nyújtás és nyírás. 

Őskép
A(1|1), B(5|1), C(5|5), D(3|7), E(1|5)

Eltolás: dx=2, dy=1  ☑
A1(3|2), B1(7|2), C1(7|6), D1(5|8), E1(3|6)

Forgatás: Z(2|-1), α=-60°  ☑
A2(5,0981|-0,36603), B2(7,0981|-3,8301),    
C2(10,562|-1,8301), D2(11,294|0,90192), 
E2(8,5622|1,634)

Kör és körrészek

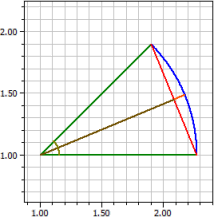
Ha a következő adatok közül kettő adott, a program kiszámítja a többit. 

Adott:
¯¯¯¯¯¯¯¯      
                 Ív b = 1
                Szög α = 45°

Eredmények :
¯¯¯¯¯¯¯¯¯¯
                Sugár r = 1,2732395
                Húr s = 0,97449536
      Körcikk A1 = 0,63661977
             Távolság d = 1,17632
           Nyílmagasság h = 0,096919589                
 Körszelet A2 = 0,063460604

        Kör területe A = 5,0929582
      Kör kerülete u = 8

Érintőkörök   (Új a 9.0 verzióban, 2021 februártól)

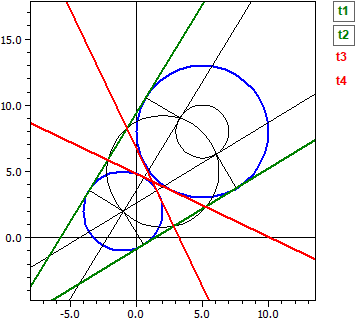
A program kiszámítja a következő érintők egyenleteit:

  • Érintő egy körhöz k egy pontban B
  • Érintők egy körhöz k egy P ponton keresztül a körön kívül
  • Érintők egy körhöz k párhuzamosan egy g egyenessel
  • Érintők két körhöz k1 és k2
Adott:
¯¯¯¯¯¯¯¯
  k1 : M(5|8) ,   r =5
  k2 : M(-1|2) ,   r =3

Külső érintők
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t1: -4,2923·x + 7,04104·y = -6,36427
  t2: -7,04104·x + 4,29230·y = 40,3643

Belső érintők
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t3: 1,21895·x + 2,55228·y = 12,3709
  t4: -2,55228·x − 1,21895·y = -8,3709

Síkbeli metszetek

A program kiszámítja egyenesek és körök metszéspontjait

két egyenes

g : x + y = 0
h : x - y = 5

Metszéspont : S(2,5|-2,5)

Metszési szög: 90°

Távolságok az origótól :
  d(g,O) = 0
  d(h,O) = 3,5355339

Egyenes és kör

k : M(5|0)   r = 5
g : x + y = 0

Metszéspontok :
  S1(5|-5)    S2(0|0)     

Két kör

k1 : M1(5|5)   r1 = 5
k2 : M2(0|0)   r2 = 5

Metszéspontok :
  S1(5|0)   S2(0|5)

Összekötő egyenes :   
  x + y = 5