MatheAss 10.0 − Valószínűségszámítás

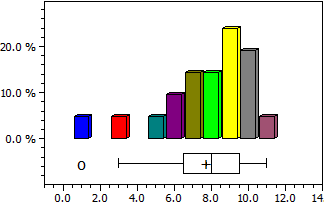
Statisztika

Egy adatsorhoz meghatározható az átlag (aritmetikai közép), a medián, a variancia és a szórás. Ezenkívül az eloszlás hisztogramként és box-plotként kerül ábrázolásra.

Adatok:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8

Adatok száma          n = 21
Maximum              max = 11
Minimum              min = 1
Átlag                         x = 7,7142857
Medián                       c = 8
Variancia                    s² = 6,1142857
Szórás                       s = 2,4727082

Regresszió

Ezzel a rutinnal egy mérési sorozathoz illesztett görbe számítható. A következő illesztések közül lehet választani, és szükség esetén az összes pont x- vagy y-iránnyal eltolható, illetve nyújtható.

Eredetegyenes ( y = a·x )

Lineáris regresszió ( y = a·x + b )

n-ed rendű polinomregresszió ( y = a₀ + ... + a_n·xⁿ )

Geometriai regresszió ( y = a·x^b )

Exponenciális regresszió ( y = a·b^x )

Logaritmikus regresszió ( y = a + b·ln(x) )

Az ábrával együtt megjelenik az illesztett függvény kifejezése, a determinációs együttható, a korrelációs együttható és a szórás.

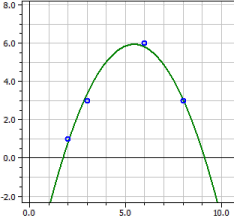
Polinomregresszió

y =  − 2,6299435
      + 3,8516949·x
      − 0,43361582·x²

Determinációs együttható = 0,98338318
Korrelációs együttható   = 0,99165679        
Szórás                   = 0,46028731

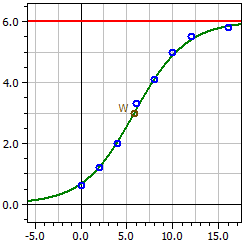
Logisztikus regresszió (Új a 9.0 verzióban)

A program egy mérési sorozathoz illesztést végez a logisztikus függvényre
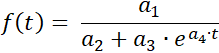
a következő paraméterekkel: a₁ = ƒ(0)·S , a₂ = ƒ(0) , a₃ = S - ƒ(0) , és a₄ = -k·S , valamint a telítési határ S .

Adatok forrása: "Hopfenwachstum.csv"

Telítési határ: 6
         Rejtett érték: 1

                                 4,0189
ƒ(x) = ————————————————
             0,66981 + 5,3302 · e^(-0,35622·t)

Inflexiós pont W(5,8226/3)

Maximális növekedési ráta  ƒ'(xw) = 0,53433

8 érték 
Determinációs együttható = 0,99383916
Korrelációs együttható   = 0,99691482
Szórás                   = 0,16172584

Kombinatorika

Kiszámítja annak lehetőségeit, hogy n elemből k elemet válasszunk, figyelembe véve vagy figyelmen kívül hagyva a sorrendet, és engedélyezve vagy tiltva az ismétléseket.

n = 49 ,  k = 6

Rendezett választás ismétlés nélkül = 10 068 347 520
Rendezett választás ismétléssel     = 13 841 287 201
Rendezetlen választás ismétlés nélkül = 13 983 816
Rendezetlen választás ismétléssel     = 25 827 165

Permutációk k esetén:                k ! = 720

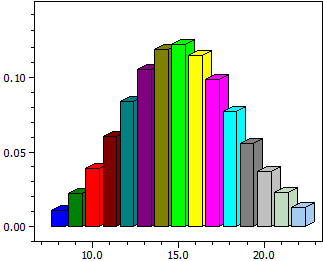
Binomiális eloszlás

Kiszámítja egy b(k;n;p) eloszlású valószínűségi változó X értékeit rögzített n és p mellett.

- oszlopdiagramot a valószínűségekről P( X = k )
- numerikus értékeit egy [k-min;k-max] intervallumban
- a valószínűséget P( k-min <= X <= k-max )

n = 50             p = 0,3

    k             P(X=k)         P(0<=X<=k) 
  ¯¯¯¯    ¯¯¯¯¯¯¯¯¯¯     ¯¯¯¯¯¯¯¯¯¯
    8         0,01098914     0,01825335
    9         0,02197829     0,04023163
  10        0,03861899     0,07885062
  11        0,06018544     0,13903606
  12        0,08382972     0,22286578
  13        0,10501745     0,32788324
  14        0,11894834     0,44683157
  15        0,12234686     0,56917844
  16        0,11470018     0,68387862
  17        0,09831444     0,78219306
  18        0,07724706     0,85944012
  19        0,05575728     0,91519740
  20        0,03703876     0,95223616
  21        0,02267679     0,97491296
  22        0,01281092     0,98772387
  ¯¯¯¯    ¯¯¯¯¯¯¯¯¯¯     ¯¯¯¯¯¯¯¯¯¯
  P(8<=k<=22) =            0,98045967

Hipergeometrikus eloszlás

Kiszámítja egy h(k;n;m;r) eloszlású valószínűségi változó X értékeit rögzített n, m és r mellett, oszlopdiagramot és táblázatot adva a valószínűségekről P( X = k ).

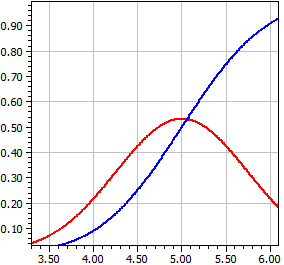
Normáleloszlás

Kiszámítja egy N(μ,σ²) eloszlású valószínűségi változó X értékeit, adott várható érték μ és variancia σ² mellett, a sűrűségfüggvényt ƒ(x) és az eloszlásfüggvényt Φ(x), vagyis az ƒ(x) integrálját.

  μ = 5              σ = .75

      x                      ƒ(x)                Φ(x)   
  ¯¯¯¯¯¯¯¯¯¯  ¯¯¯¯¯¯¯¯¯¯  ¯¯¯¯¯¯¯¯¯¯
  2                    0,00017844   0,00003167
  2,33333333   0,00095649   0,00018859
  2,66666666   0,00420802   0,00093192
  2,99999999   0,01519465   0,00383038
  3,33333332   0,04503153   0,01313415
  3,66666665   0,10953585   0,03772017
  3,99999998   0,21868009   0,09121120
  4,33333331   0,35832381   0,18703139
  4,66666664   0,48189843   0,32836063
  4,99999997   0,53192304   0,49999998
  5,3333333     0,48189845   0,67163934
  5,66666663   0,35832383   0,81296859
  5,99999996   0,21868012   0,90878878
  6,33333329   0,10953586   0,96227982
  6,66666662   0,04503154   0,98686585
  6,99999995   0,01519465   0,99616962
  7,33333328   0,00420802   0,99906808
  7,66666661   0,00095649   0,99981141
  7,99999994   0,00017844   0,99996833