MatheAss 10.0 − Algebra

Primtall

Programmet beregner alle primtall mellom to tall.

Primtall mellom 1000000000 og 1000000300:

1000000007 1000000009 1000000021 1000000033 1000000087 1000000093
1000000097 1000000103 1000000123 1000000181 1000000207 1000000223
1000000241 1000000271 1000000289 1000000297

16 primtall

Primtallspar   (Nytt i versjon 9.0)

Programmet finner i et intervall [a,b] alle primtallstvillinger (p,p+2), primtallsfettere (p,p+4), Sexy Primes (p,p+6) og primtallstrillinger.

Primtallstrillinger mellom 1 og 200

(3|5|7) (5|7|11) [7|11|13] (11|13|17) [13|17|19] (17|19|23) [37|41|43] 
(41|43|47) [67|71|73] [97|101|103] (101|103|107) [103|107|109] (107|109|113)
(191|193|197) [193|197|199] 

15 tripler med primtallstrillinger
7 av typen (p|p+2|p+6) og 7 av typen [p|p+4|p+6]

opp Primfaktorisering

Programmet deler naturlige tall opp i sine primtallspotens. 

  99999999999901 = 19001 · 5262880901
  99999999999001 = 107 · 401 · 1327 · 1756309
  99999999990001 = primtall 
    3938980639167 = 314 · 77
999330136292431 = 999712 · 99991

opp største felles divisor og minste felles multiplum

For to tall a og b bestemmes den største felles divisor, det minste felles multiplum og deres mengder av delere. 

a = 24
b = 256

største felles divisor                     gcd = 8
minste felles multiplum                 lcm = 768  

Delermengder :
T(a) = { 1 2 3 4 6 8 12 24}
T(b) = { 1 2 4 8 16 32 64 128 256}

opp Prosentregning   (Nytt i versjon 9.0)

Programmet beregner grunnverdi G, prosentverdi W, prosentsats p eller p%, vekstfaktor q og sluttverdi E, når to uavhengige av disse er gitt.

Gitt:
¯¯¯¯¯¯¯¯
Prosentverdi  W = −120
    Vekstfaktor  q = 95% = 0,95 = 19/20

Resultater:
¯¯¯¯¯¯¯¯¯¯
    Grunnverdi  G = 2400
Prosentsats  p% = −5% = −0,05 = −1/20      
      Sluttverdi  E = 2280

opp Desimaltall til brøk

Programmet konverterer periodiske og endelige desimalbrøk til brøk. 

Ikke-periodisk del : 1.20
Periode : 045
    ___
1.20045 = 120/100 + 1/2220 = 533/444

opp Brøk til desimaltall

Programmet konverterer brøk til periodiske desimalbrøk og bestemmer perioden og dens lengde. 

Teller : 533
Nevner : 444
              ___
533/444 = 1.20045
periodisk fra den 3. posisjonen etter komma
perioden er 3 sifre lang

opp Binomer

Blant de mest kjente formlene i skolematematikk er sikkert den binomiske formelen (a + b)² = a² + 2ab + b² .

Programmet beregner det mer generelle tilfellet (a·x + b·y)n. 

(2·x  − 3·y)7 =       +128 · x7
                           −1344 · x6 · y
                            +6048 · x5 · y2
                          −15120 · x4 · y3   
                          +22680 · x3 · y4
                          −20412 · x2 · y5
                          +10206 · x · y6
                            −2187 · y7

opp Ligninger av 4. grad

Programmet bestemmer de reelle løsningene til en ligning av 4. eller lavere grad. For ligninger av høyere grad finnes det, bortsett fra tilnærmede beregninger (nullpunkter i kurvediskusjon), ingen algebraisk løsningsmetode. 

x4 + 2·x3 - 3·x2 + 5·x - 5 = 0   <=>   (x - 1)·(x3 + 3·x2 + 5) = 0
L = {-3,42599;  1}

opp Diofantiske ligninger

Oppkalt etter Diophantos fra Alexandria (ca. 250), som i sin bok Arithmetica behandlet løsning av lineære og kvadratiske ligninger, spesielt deres heltallige løsninger.
Programmet beregner de heltallige løsningene til ligningen  a·x - b·y - c = 0. Dermed kan man bestemme de heltallige punktene på en linje. 

7·x − 3·y − 5 = 0 ;   x,y heltallige
L = { ( 2 + 3t | 3 + 7t ) }

opp Pythagoreiske talltrippel

Pythagoreiske talltrippel er de heltallige løsningene (x,y,z) av ligningen x² + y² = z² , som gjelder for sidene i rettvinklede trekanter.

For x, y, z mellom 100 og 400 får man:

( 119, 120, 169 )    ( 104, 153, 185 )    ( 133, 156, 205 )    ( 105, 208, 233 )    
( 140, 171, 221 )    ( 115, 252, 277 )    ( 120, 209, 241 )    ( 161, 240, 289 )    
( 160, 231, 281 )    ( 207, 224, 305 )    ( 175, 288, 337 )    ( 135, 352, 377 )    
( 136, 273, 305 )    ( 204, 253, 325 )    ( 225, 272, 353 )    ( 189, 340, 389 )    
( 180, 299, 349 )    ( 252, 275, 373 )    ( 152, 345, 377 )    ( 228, 325, 397 )

opp Kalkulatorer

Det finnes fire kalkulatorer:

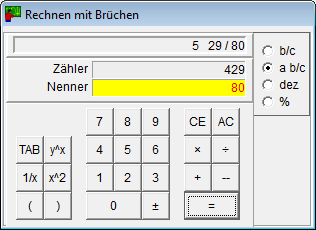
  • Kalkulatoren for brøk behersker de fire grunnleggende regneartene og kan potensere.
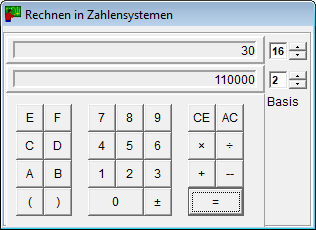
  • Kalkulatoren for tallsystemer regner med enhver base mellom 2 og 16.
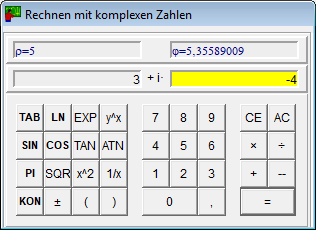
  • Kalkulatoren for komplekse tall beregner i tillegg til de vanlige funksjonene også det konjugerte komplekse av et tall.
  • Kalkulatoren for store heltall behersker de grunnleggende regneartene og kombinatoriske formler.
TR TR TR

Regning med store tall (Nytt i versjon 9.0 fra april 2021)

Det regnes med heltall med maksimalt 10 000 sifre.

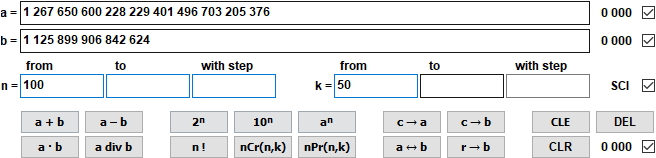
1 267 650 600 228 229 401 496 703 205 376   div  1 125 899 906 842 624  
 =  1 125 899 906 842 624  Rest  0
 =  1,13 · 10^15 Rest 0

nCr(100,50)  =  100 891 344 545 564 193 334 812 497 256 = 1,01 · 10^29