MatheAss 10.0 − Analyse

Følger og rekker (Nytt i versjon 9.0 fra mai 2021)

Programmet bestemmer de første n leddene i en følge (a_i) og den tilhørende rekken (summen av følgeleddene), når de første leddene i følgen og en eksplisitt funksjon a_i=ƒ(i) eller en rekursjonsformel a_i=ƒ(a₀, a₁, ... , a_i-1) er gitt.

a[0]=1;   a[1]=1;   a[ i ] = a[i-1] + a[i-2];   n = 20

Følge
¯¯¯¯¯
( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765)

Rekke
¯¯¯¯¯
( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)

Polynomdivisjon

Programmet beregner produktet og kvotienten av to polynomer.

1. Polynom:  3·x⁴ - 2·x + 1
2. Polynom:  2·x + 5

      Produkt:  6·x⁵ + 15·x⁴ - 4·x² - 8·x + 5                 
     Kvotient:  3/2·x³ - 15/4·x² + 75/8·x - 391/16
           Rest:  1971/16

Faktorisering av polynomer (Nytt i versjon 9.0)

Programmet beregner de rasjonale nullpunktene og lineær faktoriseringsformen til et polynom.

p(x) = x⁵ - 9·x⁴ - 82/9·x³ + 82·x² + x - 9
       = (1/9)·(9·x⁵ - 81·x⁴ - 82·x³ + 738·x² + 9·x - 81)
       = (1/9)·(3·x - 1)·(3·x + 1)·(x - 9)·(x - 3)·(x + 3)

Rasjonale nullpunkter: 1/3, -1/3, 9, 3, -3

Polynomtransformasjon (Nytt i versjon 9.0)

En polynomfunksjon ƒ(x) kan forskyves eller strekkes i x-retning og y-retning.

ƒ(x) =  - 1/4·x⁴ + 2·x³ - 16·x + 21

Forskyvning med dx = -2 ,  dy = 0                             

ƒ(x + 2) =  - 1/4·x⁴ + 6·x² + 1

Største felles divisor og minste felles multiplum av polynomer (Nytt i versjon 9.0 fra februar 2021)

Programmet beregner den største felles divisor (ggT) og det minste felles multiplum (kgV) av to polynomer p₁(x) og p₂(x).

p₁(x) =  4·x⁶ - 2·x⁵ - 6·x⁴- 18·x³ - 2·x² + 24·x + 8
p₂(x) =  10·x⁴- 14·x³ - 22·x² + 14·x + 12

ggT(p₁,p₂) =  x² - x - 2
kgV(p₁,p₂) =  40·x⁸ - 36·x⁷ - 76·x⁶ - 144·x⁵ + 88·x⁴+ 356·x³ - 4·x² - 176·x - 48

Funksjonsplotter 1

Det kan tegnes opptil ti funksjoner samtidig i et koordinatsystem. Tillatt er også kombinasjoner eller derivasjoner av allerede definerte funksjoner.

La  ƒ₁(x)=sin(x) og ƒ₂(x)=3*sqrt(x), da blir

ƒ₃(x)=2*y1^2-y2         ƒ₃(x)=2*sin(x)^2-3*sqrt(x)
ƒ₄(x)=f2(y1)               ƒ₄(x)=3*sqrt(sin(x))
ƒ₅(x)=y2'                   ƒ₅(x)=3/(2*sqrt(x))

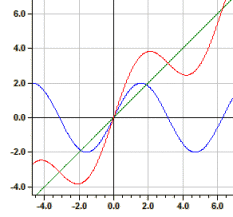
Eksempel: ƒ₁(x)=sin(x), ƒ₂(x)=x og ƒ₃(x)=y1+y2

Funksjonsplotter 2

Her tegnes en stykkevis definert funksjon, gitt ved ni del-funksjoner. For hver del-funksjon angis definisjonsområdet, typen intervall og fargen. I tillegg kan man bestemme om randpunktene skal tegnes eller ikke.

Eksempel:

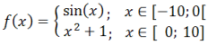
Parameterkurver

Med dette programmet kan man tegne kurver som ikke er gitt ved et eksplisitt funksjonsuttrykk, men gjennom to funksjoner for den horisontale og vertikale forskyvningen.

Eksempel: Lissajous-figurer

x(k) = sin(3*k)

y(k) = cos(5*k)

k fra -Pi til Pi

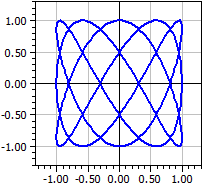
Lissajous-figurer får man ved å koble to vekselspenninger med ulik frekvens til et oscilloskop.

Kurvefamilier

Programmet tegner grafene til vilkårlige funksjoner som inneholder en parameter k. Verdiene for k kan listes opp eller bestemmes ved startverdi, sluttverdi og trinnstørrelse.

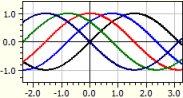
ƒ(x,k) = sin(x+k)

k fra -2 til 2 med trinnstørrelse Pi/4

Polynomfunksjoner (Nytt i versjon 9.0)

Programmet utfører en kurvediskusjon for en helt rasjonell funksjon (polynomfunksjon). Det vil si at derivasjonene og stamfunksjonen (integrasjonen) bestemmes, og funksjonen undersøkes for rasjonale nullpunkter, ekstrema, vendepunkter og symmetri.

Funksjon :
¯¯¯¯¯¯¯¯
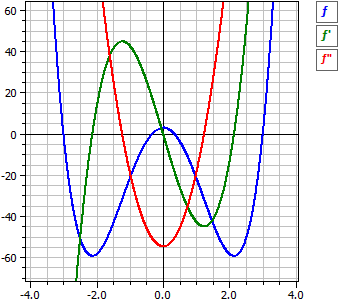
ƒ(x) = 3·x⁴ - 82/3·x² + 3
       = 1/3·(9·x⁴ - 82·x² + 9)
       = 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)                  

Derivasjoner :
¯¯¯¯¯¯¯¯¯¯
ƒ'(x)  = 12·x³ - 164/3·x
ƒ"(x)  = 36·x² - 164/3
ƒ'"(x) = 72·x

Stamfunksjon
¯¯¯¯¯¯¯¯¯¯¯¯
ƒ(x) = 3/5·x⁵ - 82/9·x³ + 3·x + c

  .
  .
  .

Rasjonale funksjoner (Nytt i versjon 9.0)

Programmet utfører kurvediskusjon for en (brøkt)rasjonal funksjon. Det vil si at derivasjonene, definisjonslukene og den kontinuerlige forlengelsen bestemmes. Funksjonen undersøkes for nullpunkter, ekstrema, vendepunkter og oppførsel for |x|→ ∞.

Funksjon :
¯¯¯¯¯¯¯¯
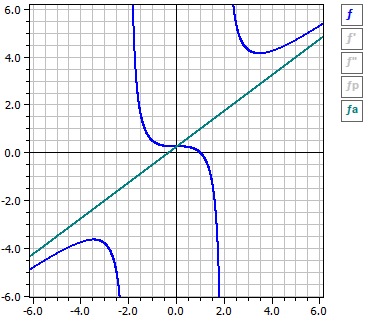
            3·x³ + x² - 4         (x - 1)·(3·x² + 4·x + 4)  
ƒ(x) = —————— = ———————————
               4·x² - 16                4·(x - 2)·(x + 2)       

Definisjonsluker
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x = 2  Pol med fortegnsskifte
x =-2  Pol med fortegnsskifte

Derivasjoner :
¯¯¯¯¯¯¯¯¯¯
               3·(x⁴ - 12·x²)             3·(x²·(x² - 12))   
ƒ'(x) = ———————— = —————————
            4·(x⁴ - 8·x² + 16)       4·(x - 2)²·(x + 2)² 

                     6·(x³ + 12·x)                6·(x·(x² + 12))  
ƒ"(x) = ——————————— = ————————
             x⁶ - 12·x⁴ + 48·x² - 64        (x - 2)³·(x + 2)³ 

  .
  .
  .

Kurvediskusjon

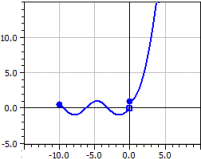
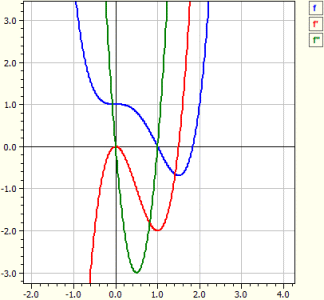
Programmet utfører kurvediskusjon for en vilkårlig funksjon. Det vil si at derivasjonene bestemmes, funksjonen undersøkes for nullpunkter, ekstrema og vendepunkter, grafene til ƒ, ƒ' og ƒ" tegnes, og en verditabell genereres.

Funksjon :
‾‾‾‾‾‾‾‾‾‾‾‾‾
  ƒ(x) = x^4 - 2*x^3 + 1
  Undersøkelse i området fra  -10  til  10                

Derivasjoner:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  ƒ'(x) = 4*x^3-6*x^2
  ƒ"(x) = 12*x^2-12*x

Nullpunkter:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  N₁( 1 | 0 )                  m = -2
  N₂( 1,83929 | 0 )       m =  4,5912

Ekstrema:
‾‾‾‾‾‾‾‾‾‾‾‾
  T₁( 1,5 |-0,6875 )      m = 0

Vendepunkter:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
  W₁( 0 | 1 )                 m = 0
  W₂( 1 | 0 )                 m =-2

Newton-iterasjon

Newton-iterasjon er en tilnærmet metode for å beregne en nullpunktløsning av ƒ(x). Dersom man gir en startverdi x₀ som ligger nær nok den søkte nullpunktet, beregnes neste tilnærming som skjæringspunktet mellom tangenten til grafen til ƒ i punktet P(x₀ / ƒ(x₀)).

  ƒ(x) = x-cos(x)

                 x                       ƒ(x)                  ƒ'(x) 
   ————————   ——————   ——————   
   x₀ = 1
   x₁ = 0,75036387     0,45969769       1,841471
   x₂ = 0,73911289     0,018923074     1,681905
   x₃ = 0,73908513     0,00004646       1,6736325
   x₄ = 0,73908513     0,00000000       1,673612

Integralregning (fra februar 2021 med buelengder)

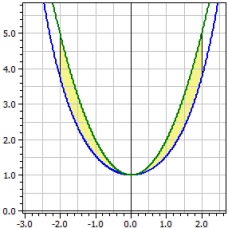
Her beregnes det orienterte og det absolutte arealet mellom to funksjonskurver i et gitt intervall. I tillegg bestemmes:
- dreieøyeblikk ved rotasjon rundt x- eller y-aksen,
- de overstrøkne rotasjonsvolumene,
- buelengdene i intervallet [a;b], og
- tyngdepunktet til flaten (når A1=A2).

  ƒ₁(x) = cosh(x)
  ƒ₂(x) = x^2+1

  Integrasjonsintervall  [a;b]  fra  -2 til 2

  Orientert areal :  A₁ = -2,07961
  Absolutt areal  :  A₂ = 2,07961

  Buelengder      :  L₁[a;b] = 7,254    L₂[a,b] = 9,294

Rekkeutvikling

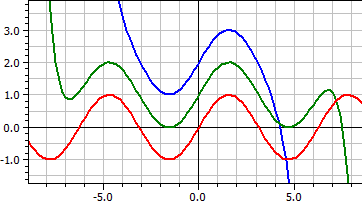
Her tegnes en funksjon gitt som en rekke, hvor rekkeutviklingene for ulike parameterområder sammenlignes og kan forskyves i y-retning for bedre tydelighet.

De første 16 leddene i Taylor-rekken 
for sinusfunksjonen.

ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) ,   
k = 4, 8 og 16

Flatefunksjoner

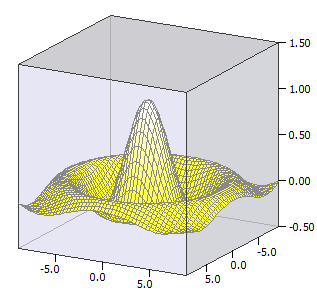
Her tegnes en flatefunksjon ƒ(x,y), det vil si det tredimensjonale grafiske bildet av en funksjon med to variabler.

Eksempel:

ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)

-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5