MatheAss 10.0 − Stokastikk

Statistikk

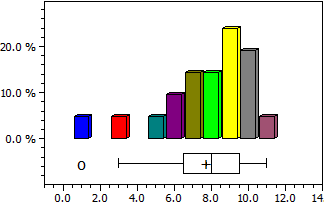
For en dataliste beregnes gjennomsnitt (aritmetisk middel), median, varians og standardavvik. I tillegg vises fordelingen som histogram og som boksplott. 

Data:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8

Antall data                 n = 21
Maksimum            max = 11
Minimum                min = 1
Gjennomsnitt             x = 7,7142857
Median                      c = 8
Varians                     s² = 6,1142857
Standardavvik          s = 2,4727082

Regresjon

Med denne rutinen kan du utføre en kurvetilpasning til en måleserie. Du kan velge mellom følgende tilpasninger og ved behov forskyve eller strekke alle punkter i x- eller y-retning.

Ursprungsrett linje   ( y = a·x )

Lineær regresjon   ( y = a·x + b )

Polynomregresjon av n-te orden   ( y = a0 + ... + an·xn )

Geometrisk regresjon   ( y = a·xb )

Eksponentiell regresjon   ( y = a·bx )

Logaritmisk regresjon   ( y = a + b·ln(x) )

Sammen med grafen vises funksjonsuttrykket til tilpasningskurven, bestemmelsesgraden, korrelasjonskoeffisienten og standardavviket. 

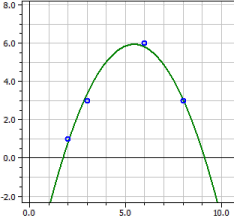
Polynomregresjon

y =  − 2,6299435
      + 3,8516949·x
      − 0,43361582·x2

Bestemmelsesgrad    = 0,98338318
Korrelasjonskoeff.      = 0,99165679        
Standardavvik            = 0,46028731

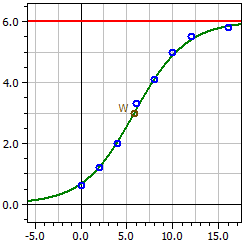
Logistisk regresjon   (Nytt i versjon 9.0)

Programmet utfører en kurvetilpasning til den logistiske funksjonen  
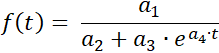
med parameterne    a1 = ƒ(0)·S ,  a2 = ƒ(0) ,  a3 = S - ƒ(0) ,  og  a4 = -k·S  samt metningsgrensen S .

Data fra: "Hopfenwachstum.csv"

Metningsgrense: 6
         Mørketall: 1

                                 4,0189
ƒ(x) = ————————————————
             0,66981 + 5,3302 · e^(-0,35622·t)

Vendepunkt W(5,8226/3)

Maksimal vekstrate  ƒ'(xw) = 0,53433

8 verdier 
Bestemmelsesgrad    = 0,99383916
Korrelasjonskoeff      = 0,99691482
Standardavvik           = 0,16172584

Kombinatorikk

Her beregnes antallet muligheter for å velge ut k elementer fra n, avhengig av om rekkefølgen har betydning eller ikke, og om gjentakelser er tillatt eller ikke. 

n = 49 ,  k = 6

Ordnet utvalg uten gjentakelse   = 10 068 347 520
Ordnet utvalg med gjentakelse   = 13 841 287 201
Uordnet utvalg uten gjentakelse = 13 983 816
Uordnet utvalg med gjentakelse = 25 827 165

Permutasjoner av k :                k ! = 720

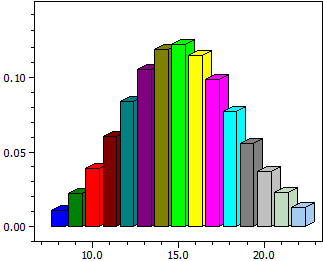
Binomialfordeling

For en b(k;n;p)-fordelt tilfeldig variabel X med fast n og fast p beregnes

- et stolpediagram for sannsynlighetene P( X = k )
- deres numeriske verdier i et intervall [k-min;k-max]
- sannsynligheten P( k-min <= X <= k-max) 

n = 50             p = 0,3

    k             P(X=k)         P(0<=X<=k) 
  ¯¯¯¯    ¯¯¯¯¯¯¯¯¯¯     ¯¯¯¯¯¯¯¯¯¯
    8         0,01098914     0,01825335
    9         0,02197829     0,04023163
  10        0,03861899     0,07885062
  11        0,06018544     0,13903606
  12        0,08382972     0,22286578
  13        0,10501745     0,32788324
  14        0,11894834     0,44683157
  15        0,12234686     0,56917844
  16        0,11470018     0,68387862
  17        0,09831444     0,78219306
  18        0,07724706     0,85944012
  19        0,05575728     0,91519740
  20        0,03703876     0,95223616
  21        0,02267679     0,97491296
  22        0,01281092     0,98772387
  ¯¯¯¯    ¯¯¯¯¯¯¯¯¯¯     ¯¯¯¯¯¯¯¯¯¯
  P(8<=k<=22) =            0,98045967

Hypergeometrisk fordeling

For en h(k;n;m;r)-fordelt tilfeldig variabel X med fast n, m og r beregnes et stolpediagram og en verditabell for sannsynlighetene P( X = k ).

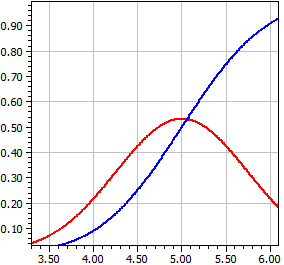
Normalfordeling

For en N(µ,σ²)-fordelt tilfeldig variabel X med gitt forventningsverdi µ og varians σ² beregnes tetthetsfunksjonen ƒ(x) og fordelingsfunksjonen Φ(x), det vil si integralet over ƒ(x) .

  μ = 5              σ = .75

      x                      ƒ(x)                Φ(x)   
  ¯¯¯¯¯¯¯¯¯¯  ¯¯¯¯¯¯¯¯¯¯  ¯¯¯¯¯¯¯¯¯¯
  2                    0,00017844   0,00003167
  2,33333333   0,00095649   0,00018859
  2,66666666   0,00420802   0,00093192
  2,99999999   0,01519465   0,00383038
  3,33333332   0,04503153   0,01313415
  3,66666665   0,10953585   0,03772017
  3,99999998   0,21868009   0,09121120
  4,33333331   0,35832381   0,18703139
  4,66666664   0,48189843   0,32836063
  4,99999997   0,53192304   0,49999998
  5,3333333     0,48189845   0,67163934
  5,66666663   0,35832383   0,81296859
  5,99999996   0,21868012   0,90878878
  6,33333329   0,10953586   0,96227982
  6,66666662   0,04503154   0,98686585
  6,99999995   0,01519465   0,99616962
  7,33333328   0,00420802   0,99906808
  7,66666661   0,00095649   0,99981141
  7,99999994   0,00017844   0,99996833