MatheAss 10.0 − 3-dim. Geometri
Koordinatsystemer
Med dette programmet kan man omregne tredimensjonale kartesiske koordinater til kulekoordinater eller sylinderkoordinater og omvendt.
kartesisk polar sylindrisk x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Platoniske kropper
Programmet beregner de fem platoniske kroppene Tetraeder, Heksaeder, Oktader, Dodekaeder og Ikosaeder, når kantelengde, flatehøyde, romhøyde, innkuleradius, omkuleradius, volum eller overflate er gitt.
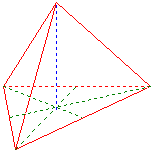
Tetraeder
Gitt:
¯¯¯¯¯¯¯¯
Omkuleradius ru = 1
Resultater:
¯¯¯¯¯¯¯¯¯¯
Kant a = 1,6329932
Flatehøyde h1 = 1,4142136
Romhøyde h2 = 1,3333333
Innkuleradius ri = 0,33333333
Volum V = 0,51320024
Overflate O = 4,6188022
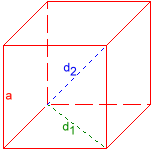
Heksaeder
Gitt:
¯¯¯¯¯¯¯¯
Overflate O = 8
Resultater:
¯¯¯¯¯¯¯¯¯¯
Kant a = 1,1547005
Flatediagonal d1 = 1,6329932
Romdiagonal d2 = 2
Omkuleradius ru = 1
Innkuleradius ri = 0,57735027
Volum V = 1,5396007
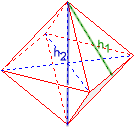
Oktader
Gitt:
¯¯¯¯¯¯¯¯
Volum V = 4/3
Resultater:
¯¯¯¯¯¯¯¯¯¯
Kant a = 1,4142136
Flatehøyde h1 = 1,2247449
Romhøyde h2 = 2
Omkuleradius ru = 1
Innkuleradius ri = 0,57735027
Overflate O = 6,9282032
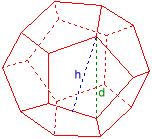
Dodekaeder
Gitt:
¯¯¯¯¯¯¯¯
Flatediagonal d = 2
Resultater:
¯¯¯¯¯¯¯¯¯
Kant a = 1,236068
Flatehøyde h = 1,902113
Omkuleradius ru = 1,7320508
Innkuleradius ri = 1,3763819
Volum V = 14,472136
Overflate O = 31,543867
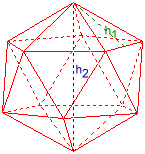
Ikosaeder
Gitt:
¯¯¯¯¯¯¯¯
Romhøyde h2 = 2
Resultater:
¯¯¯¯¯¯¯¯¯
Kant a = 1,0514622
Flatehøyde h1 = 0,910593
Omkuleradius ru = 1
Innkuleradius ri = 0,79465447
Volum V = 2,5361507
Overflate O = 9,5745414
Andre kropper
Programmet beregner alle størrelser til et regelmessig prisme, en rett sirkelsylinder, en kvadratisk pyramide, en rett sirkelskjegle eller en kule, når to av dem er gitt.
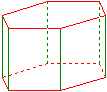
Prismet
Gitt: n = 4
¯¯¯¯¯¯¯¯
Volum V = 1
Overflate O = 6
Resultater:
¯¯¯¯¯¯¯¯¯
Side a = 1
Høyde h = 1
Omsirkelsradius ru = 0,70710678
Innsirkelsradius ri = 0,5
Grunnflate G = 1
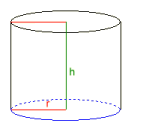
Sirkelsylinderen
Gitt:
¯¯¯¯¯¯¯¯
Radius r = 1
Volum V = 1
Resultater:
¯¯¯¯¯¯¯¯¯¯
Høyde h = 0,31830989
Omkrets u = 6,2831853
Grunnflate G = 3,1415927
Mantelflate M = 2
Overflate O = 8,2831853
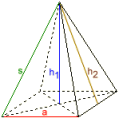
Den kvadratiske pyramiden
Gitt:
¯¯¯¯¯¯¯¯
Grunnkant a = 1
Volum V = 1
Resultater:
¯¯¯¯¯¯¯¯¯
Sidekant s = 3,082207
Romhøyde h1 = 3
Sidehøyde h2 = 3,0413813
Overflate O = 7,0827625
Sideflate A = 1,5206906
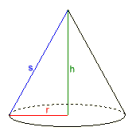
Sirkelskjeglen
Gitt:
¯¯¯¯¯¯¯¯
Volum V = 1
Grunnflate G = 1
Resultater:
¯¯¯¯¯¯¯¯¯¯
Radius r = 0,56418958
Høyde h = 3
Mantellinje s = 3,0525907
Mantelflate M = 5,4105761
Overflate O = 6,4105761
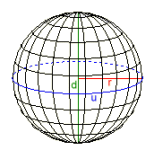
Kulen
Gitt:
¯¯¯¯¯¯¯¯
Overflate O = 1
Resultater:
¯¯¯¯¯¯¯¯¯¯
Radius r = 0,28209479
Diameter d = 0,56418958
Omkrets u = 1,7724539
Volum V = 0,094031597
Linje gjennom 2 punkter
Linje A(1|1|1), B(2|5|6)
Parameterframstilling
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
x = ⎪ 1 ⎪ + t·⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 5 ⎭
Avstand fra origo
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 0,78679579
Forhold til xy-planet
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
senkr.proj: 4·x - y = 3
Skjærpunkt: S1(0,8|0,2|0)
Skjærevinkel: 50,490288°
Forhold til yz-planet
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
senkr.proj: 5·x - 4·y = 1
Skjærpunkt: S2(0|-3|-4)
Skjærevinkel: 8,8763951°
Forhold til xz-planet
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
senkr.proj: 5·x - y = 4
Skjærpunkt: S3(0,75|0|-0,25)
Skjærevinkel: 38,112927°
Plan gjennom 3 punkter
Plan gjennom punktene:
A(1|2|3), B(2|3|3), C(1|0|1)
Punkt-retningsform:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
Koordinatligning:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Avstand fra origo:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Sporpunkter:
¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)
Kule gjennom 4 punkter
Kule gjennom punktene:
A(1|0|0), B(0|2|0),
C(0|0|3), D(1|0|1)
Normalform:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
| -> ⎧-2,5 ⎫ |2
K: | x - ⎪-0,5 ⎪ | = 12,75
| ⎩ 0,5 ⎭ |
Sentrum og radius:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-2,5|-0,5|0,5)
r = 3,5707142
Snitt i rommet
Programmet beregner skjæringer mellom linjer, plan og kuler.
to linjer
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Skjæringspunkt : S(5|5|5)
Skjærevinkel: 60°
Avstander til origo :
d(O,g)=5 d(O,h)=5
Plan og linje
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
E : x + y + z = 5
Skjæringspunkt : S(5|0|0)
Skjærevinkel: 54,73561°
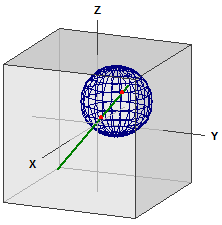
Kule og linje
-> ⎧ 1 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
K : M(5|5|5) , r = 5
Skjæringspunkter :
S1(2,8187|1,8187|1,8187)
S2(8,5147|7,5147|7,5147)
Lengde av korden :
s = 9,8657657
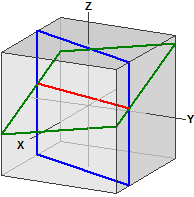
to plan
Gitt er planene:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1 : 5·x - 2·y = 5
E2 : 2·x - y + 5·z = 8
Skjærelinje mellom planene:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> |-11 | | 10 |
g : x = |-30 | + r·| 25 |
| 0 | | 1 |
Avstand fra origo:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,5057283
Skjærevinkel mellom planene:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 65,993637°
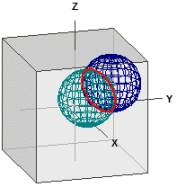
to kuler
Gitt er kulene: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ K1 : M1(3|3|3) , r1 = 3 K2 : M2(1|1|1) , r2 = 3 Skjæresirkel: ¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2), r = 2,4494897 Skjæreplan: ¯¯¯¯¯¯¯¯¯¯¯¯¯ E : x + y + z = 6
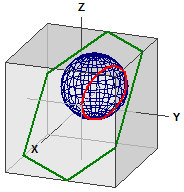
Kugel und Ebene
Plan :
¯¯¯¯¯¯¯
E : 5·x - 4·y + 5·z = -3
Kule :
¯¯¯¯¯¯¯
| -> ⎧ 1 ⎫|2
K : | x - ⎪ 2 ⎪| = 16
| ⎩ 3 ⎭|
Skjæresirkel mellom K og E :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-0,13636|2,9091|1,8636)
r = 3,548367
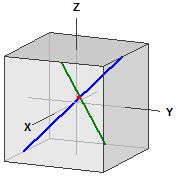
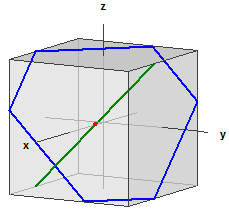
Avstander på kulen
(Nytt i versjon 9.0 fra desember 2021)
Beregner avstanden mellom to punkter på en kule. Her kombineres flere funksjoner fra MatheAss.
GPS desimal ¯¯¯¯¯¯¯¯¯¯¯ Berlin : 52.523403, 13.4114 New York : 40.714268, -74.005974 GPS dms ¯¯¯¯¯¯¯ Berlin : 52° 31' 24.2508" N, 13° 24' 41.0400" E New York : 40° 42' 51.3648" N, 74° 0' 21.5064" W . . . Avstand ¯¯¯¯¯¯¯¯¯¯ d = r · α [rad] = 6385,112
