MatheAss 10.0 − Lineær algebra

Lineære likningssystemer

Programmet bestemmer løsningsvektoren til et system av lineære likninger med n likninger og n ukjente.

Eksempel: Søker man en parabel gjennom punktene P(1/3), Q(2/1) og R(4/9), fører dette til likningssystemet

  1·x1 + 1·x2 + 1·x3 = 3
  4·x1 + 2·x2 + 1·x3 = 1
 16·x1 + 4·x2 + 1·x3 = 9   
            
 L = ( 2; -8; 9 )

Parabelen har dermed likningen y = 2x² - 8x + 9.

Eksempel med todimensjonalt løsningsrom:

  0·x1 + 0·x2 + 2·x3 - 1·x4  =  1
  1·x1 + 1·x2 + 1·x3 + 1·x4  =  4
  2·x1 + 2·x2 - 4·x3 + 5·x4  =  5
  1·x1 + 1·x2 - 7·x3 + 5·x4  =  0

  L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }

Lineær optimering (fra februar 2022)

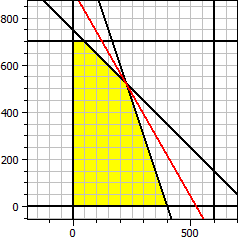
Programmet bestemmer den optimale løsningen for en målfunksjon med to variabler og lineære ulikheter som randbetingelser.

Målfunksjon:   
  ƒ(x,y) = 140·x + 80·y → Maksimum

Randbetingelser:
  x ≥ 0
  y ≥ 0
  x ≤ 600
  y ≤ 700
  x + y ≤ 750
  3·x + y ≤ 1200

Maksimum
  x = 225   y = 525
  ƒ(x,y) = 73500

Programmet bestemmer lineærkombinasjonen av en vektor fra tre gitte vektorer. Rutinen egner seg også til å undersøke den lineære uavhengigheten til tre vektorer i rommet, det vil si om de ligger i et plan.

    ⎧ 1 ⎫     ⎧ 2 ⎫     ⎧ 0 ⎫   ⎧ 2 ⎫
  a·⎪ 2 ⎪ + b·⎪ 1 ⎪ + c·⎪ 1 ⎪ = ⎪ 3 ⎪   
    ⎩ 0 ⎭     ⎩ 1 ⎭     ⎩ 0 ⎭   ⎩ 7 ⎭

Løsning :
  a = -12  b = 7  c = 20

Skalarprodukt

Programmet beregner for to vektorer deres skalarprodukt, lengden av begge vektorene og den innsluttede vinkelen.

   ->  ⎧ 1 ⎫   ->  ⎧ 5 ⎫
   a = ⎪ 3 ⎪   b = ⎪ 0 ⎪
       ⎩ 1 ⎭       ⎩ 3 ⎭

Skalarprodukt av vektorene = 8

Lengde av første vektor   = √11 = 3,3166248
Lengde av andre vektor    = √34 = 5,8309519

Innsluttet vinkel  α = 65,564402°

Vektorprodukt

Programmet beregner for to vektorer vektorproduktet samt dets beløp. Vektorproduktet står vinkelrett på parallellogrammet de spenner opp, og beløpet er lik arealet av parallellogrammet.

     ->  ⎧ 1 ⎫     ->  ⎧ 7 ⎫
     a = ⎪ 2 ⎪     b = ⎪ 1 ⎪
         ⎩ 3 ⎭         ⎩ 4 ⎭

 ->  ->  ⎧  5 ⎫    ->  ->  
 a x b = ⎪ 17 ⎪   |a x b|= √483 = 21,977261
         ⎩-13 ⎭

Spatprodukt

Programmet beregner spatproduktet av tre vektorer. Beløpet gir volumet av den forskyvde kuboiden (spat) som spennes opp av de tre vektorene.

  ->  ⎧ 2 ⎫     ->  ⎧ 2 ⎫     ->  ⎧ 3 ⎫   
  a = ⎪ 3 ⎪     b = ⎪-1 ⎪     c = ⎪ 9 ⎪
      ⎩ 5 ⎭         ⎩ 7 ⎭         ⎩ 2 ⎭

    ->  ->    ->  
  ( a x b ) · c = 26

Matriseinversjon

Programmet beregner for en kvadratisk matrise av orden n determinanten, rangen og den inverse matrisen.

Matrise: 

  ⎧  0  1  1  ⎫
  ⎪  0  1  3  ⎪
  ⎩  2  0  1  ⎭

Invers matrise

  ⎧  0,25 -0,25  0,5  ⎫
  ⎪   1,5  -0,5    0  ⎪
  ⎩  -0,5   0,5    0  ⎭

Orden = 3,  Rang = 3,  Determinant = 4

Pseudoinvers matrise

Er kolonnene i en matrise A lineært uavhengige, er A^T· A inverterbar og man får med følgende formel pseudoinversen:

A⁺ = ( A^T· A )^-1· A^T

Her er A⁺ en venstre-invers av A , det vil si det gjelder: A⁺ · A = E .

Matrise A
¯¯¯¯¯¯¯¯
  ⎧  1  1  1  1  ⎫
  ⎩  5  7  7  9  ⎭

A^T· A
¯¯¯¯¯
  ⎧  26  36  36  46  ⎫
  ⎪  36  50  50  64  ⎪
  ⎪  36  50  50  64  ⎪
  ⎩  46  64  64  82  ⎭

A^T· A ikke inverterbar

A · A^T
¯¯¯¯¯¯
  ⎧   4   28  ⎫
  ⎩  28  204  ⎭

( A · A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧  6,375 -0,875  ⎫
  ⎩ -0,875  0,125  ⎭

Høyre-invers:  A^T · ( A · A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧     2  -0,25  ⎫
  ⎪  0,25      0  ⎪
  ⎪  0,25      0  ⎪
  ⎩  -1,5   0,25  ⎭

Matrise-multiplikasjon

Programmet beregner produktmatrisen til to matriser.

 1. matrise           2. matrise

  ⎧  1  2  3  0  ⎫   ⎧  1   2   3   4  ⎫
  ⎪  4  5  6  0  ⎪   ⎪  5   6   7   8  ⎪
  ⎪  0  0  0  0  ⎪   ⎪  9  10  11  12  ⎪
  ⎩  0  0  0  0  ⎭   ⎩  0   0   0   0  ⎭

 Produktmatrise
  
  ⎧  38  44   50   56  ⎫
  ⎪  83  98  113  128  ⎪
  ⎪   0   0   0    0   ⎪
  ⎩   0   0   0    0   ⎭

MatheAss 10.0 − Lineær algebra

A+ = ( AT· A )-1· AT

A⁺ = ( A^T· A )^-1· A^T