MatheAss 10.0 − 2-dim. Geometri

Rettvinklede trekanter

Er to av de følgende størrelsene gitt, beregner programmet de andre. 

Gitt:
¯¯¯¯¯¯¯¯
 Hypot.avsnitt  p = 1,8
    Flateinnhold  A = 6 
 
Resultater:
¯¯¯¯¯¯¯¯¯¯
              Katet  a = 3
              Katet  b = 4
     Hypotenus  c = 5
            Vinkel  α = 36,869898°
            Vinkel  β = 53,130102°  
 Hypot.avsnitt  q = 3,2
           Høyde  h = 2,4

Trekanter fra tre størrelser

Fra tre ytre størrelser (sider eller vinkler) i en trekant beregner programmet sidene, vinklene, høydene, side- og vinkelhalveringslinjene, omkretsen og flateinnholdet, samt sentrum og radier til innsirkel og omsirkel. 

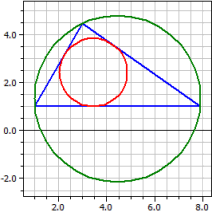
Gitt: a=6, b=4 og α=60°

      Hørn:   A(1|1)         B(7,899|1)   C(3|4,4641)
      Sider:   6                4                  6,89898
    Vinkler:   60°             35,2644°     84,7356° 
   Høyder:   3,98313      5,97469      3,4641 
    Sideh.:   4,77472      6,148          3,75513
  Vinkelh.:   4,38551      6,11664      3,5464

 Omsirkel:   M(4,44949|1,31784)       ru = 3,4641
  Innsirkel:   O(3,44949|2,41421)        ri = 1,41421

    Flate: A = 11,9494      Omkrets : u = 16,899
Trekant 2

Trekanter fra tre punkter

Fra koordinatene til tre hjørn beregner programmet alle ytre og indre størrelser (se Trekanter fra tre størrelser). 

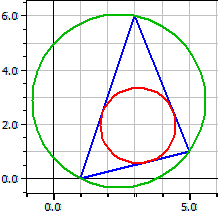
      Hørn : A(1|0)          B(5|1)          C(3|6) 
     Sider : 5,38516       6,32456       4,12311
   Vinkler : 57,5288°     82,2348°     40,2364° 
  Høyder : 4,0853        3,47851       5,33578
   Sideh. : 4,60977       3,60555       5,5 
 Vinkelh. : 4,37592       3,51849       5,46225

 Omsirkel : M(2,40909|2,86364)     ru = 3,19154
  Innsirkel : O(3,11866|1,96195)      ri = 1,38952  
   
   Flate :  A = 11            Omkrets : u = 15,8328
Trekant 3

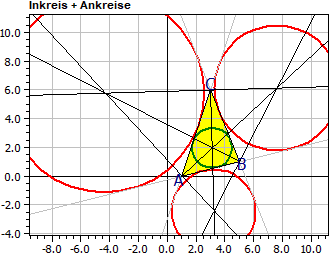
Spesielle linjer og sirkler i en trekant   (Nytt i versjon 9.0)

Programmet bestemmer likningene for midtnormalene, sidehalveringslinjene, vinkelhalveringslinjene og høydene i en trekant. Dessuten sentrum og radier til omsirkel, innsirkelen, de tre ankretsirkler og Feuerbach-sirkelen (fra mars 2025).

Gitt:
¯¯¯¯¯¯¯¯
       Hørn:    A(1|0)   B(5|1)   C(3|6)
 
Resultater:
¯¯¯¯¯¯¯¯¯¯
      Sider:   a :  5·x + 2·y = 27
                    b :  3·x - y = 3
                    c :  x - 4·y = 1
 
     Innsirkel:    Mi(3,119|1,962)         r i = 1,390
 
  Ankretsirkler: Ma(7,626|6,136)       ra = 4,346
                       Mb(-4,356|5,784)      rb = 6,910
                       Mc(3,248|-2,427)      rc = 2,900

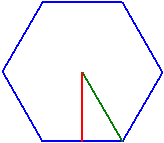
Regelmessige mangekanter

Er antall hjørn og en av de følgende størrelsene gitt, beregner programmet de andre.
Side a, innsirkelsradius ri , omsirkelsradius ru , omkrets u eller flate A.

Gitt:
¯¯¯¯¯¯¯¯
      Antall hjørn  n = 6
          Omkrets  u = 8      
 
Resultater:
¯¯¯¯¯¯¯¯¯¯
                   Side  a = 1,3333333
Omsirkelsradius ru = 1,3333333
   Innsirkelsradius ri = 1,1547005
                   Flate  A = 4,6188022                        

Vilkaårlige mangekanter   (fra november 2022)

Nå beregnes også sidene og vinklene til mangekanten, og det kontrolleres om mangekanten er konveks, konkav eller overlappende.
I tillegg kontrolleres konvekse mangekanter for om de har en innsirkel og/eller en omsirkel.

Hørn:                           Flate  A = 16
 A(1|2)                          
 B(4,5|0,5)                     Omkrets  u = 15,54498
 C(6|4)                           
 D(4,5|5,5)                     Hørnpunkt: 
 E(1|4)                           ES(3,4|3,2)

                                     Flatesenter: 
                                     FS(3,46875|3,07813)

Sider:                          Vinkler:
 |AB| = 3,8078866          ∡BAE = 113,19859°
 |BC| = 3,8078866          ∡CBA = 90°
 |CD| = 2,1213203          ∡DCB = 111,80141°
 |DE| = 3,8078866          ∡EDC = 111,80141°
 |EA| = 2                         ∡AED = 113,19859°

Sehnenmangekant
Omsirkel:  M(3,5|3)  r=2,6925824

Sehnenmangekant:

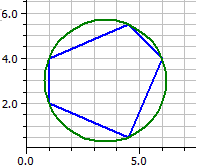
Avbildninger   (revidert i versjon 9.0)

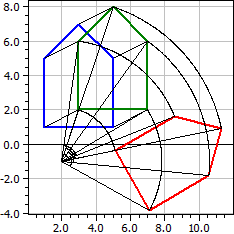
Programmet tillater å anvende en kjede av avbildninger på et n-hørn. Du kan velge mellom translasjon, linjespeiling, punktspeiling, rotasjon, sentral strekk og skjæring. 

Urfigur
A(1|1), B(5|1), C(5|5), D(3|7), E(1|5)

Translasjon: dx=2, dy=1  ☑
A1(3|2), B1(7|2), C1(7|6), D1(5|8), E1(3|6)

Rotasjon: Z(2|-1), α=-60°  ☑
A2(5,0981|-0,36603), B2(7,0981|-3,8301),    
C2(10,562|-1,8301), D2(11,294|0,90192), 
E2(8,5622|1,634)

Sirkel og sirkelbuer

Er to av de følgende størrelsene gitt, beregner programmet de andre. 

Gitt:
¯¯¯¯¯¯¯¯      
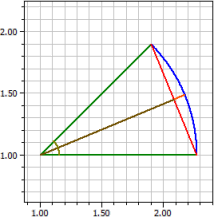
                 Bue b = 1
                Vinkel α = 45°

Resultater :
¯¯¯¯¯¯¯¯¯¯
                Radius r = 1,2732395
                Korde s = 0,97449536
      Sirkelsektor A1 = 0,63661977
             Avstand d = 1,17632
           Pilhøyde h = 0,096919589                
 Sirkelsegment A2 = 0,063460604

        Sirkelareal A = 5,0929582
      Sirkelomkrets u = 8

Sirkeltangenter   (Nytt i versjon 9.0 fra februar 2021)

Beregnes likningene for følgende tangenter:

  • Tangenten til en sirkel k i et punkt B
  • Tangentene til en sirkel k gjennom et punkt P utenfor sirkelen
  • Tangentene til en sirkel k parallelt med en linje g
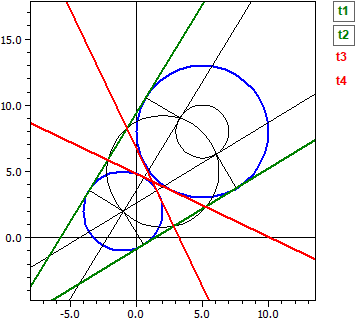
  • Tangentene til to sirkler k1 og k2
Gitt:
¯¯¯¯¯¯¯¯
  k1 : M(5|8) ,   r =5
  k2 : M(-1|2) ,   r =3

Ytre tangenter
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t1: -4,2923·x + 7,04104·y = -6,36427
  t2: -7,04104·x + 4,29230·y = 40,3643

Indre tangenter
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t3: 1,21895·x + 2,55228·y = 12,3709
  t4: -2,55228·x − 1,21895·y = -8,3709

Plan snitt

Programmet beregner skjæringene mellom linjer og sirkler

to linjer

g : x + y = 0
h : x - y = 5

Skjæringspunkt : S(2,5|-2,5)

Skjærevinkel: 90°

Avstander til origo :
  d(g,O) = 0
  d(h,O) = 3,5355339

Linje og sirkel

k : M(5|0)   r = 5
g : x + y = 0

Skjæringspunkter :
  S1(5|-5)    S2(0|0)     

to sirkler

k1 : M1(5|5)   r1 = 5
k2 : M2(0|0)   r2 = 5

Skjæringspunkter :
  S1(5|0)   S2(0|5)

Forbindelseslinje :   
  x + y = 5