MatheAss 10.0 − Algebră
Numere prime
Programul calculează toate numerele prime dintre două numere.
Numere prime între 1000000000 și 1000000300: 1000000007 1000000009 1000000021 1000000033 1000000087 1000000093 1000000097 1000000103 1000000123 1000000181 1000000207 1000000223 1000000241 1000000271 1000000289 1000000297 16 numere prime
Perechi de numere prime (Nou în versiunea 9.0)
Programul determină toate perechile de gemeni primi (p, p + 2), veri primi (p, p + 4), primi „sexy” (p, p + 6) și triplete de numere prime într-un interval [a, b].
Triplete prime între 1 și 200 (3 | 5 | 7) (5 | 7 | 11) [7 | 11 | 13] (11 | 13 | 17) [13 | 17 | 19] (17 | 19 | 23) [37 | 41 | 43] (41 | 43 | 47) [67 | 71 | 73] [97 | 101 | 103] (101 | 103 | 107) [103 | 107 | 109] (107 | 109 | 113) (191 | 193 | 197) [193 | 197 | 199] 15 triplete prime 7 de forma (p | p + 2 | p + 6) și 7 de forma [p | p + 4 | p + 6]
Descompunerea în factori primi
Programul descompune numerele naturale în puterile lor prime.
99999999999901 = 19001 5262880901
99999999999001 = 107 401 1327 1756309
99999999990001 = număr prim
3938980639167 = 3 14 7 7
999330136292431 = 99971 2 99991
CMMDC și CMMMC
Pentru două numere a și b, se determină cel mai mare divizor comun, cel mai mic multiplu comun și mulțimile divizorilor.
a = 24
b = 256
cel mai mare divizor comun cmmdc = 8
cel mai mic multiplu comun cmmmc = 768
Mulțimile divizorilor:
T(a) = { 1 2 3 4 6 8 12 24}
T(b) = { 1 2 4 8 16 32 64 128 256}
Calcularea procentelor
(nou în versiunea 9.0)
Valoarea de bază G, valoarea procentuală W, procentul p sau p%, factorul de creștere q și valoarea finală E sunt calculate dacă se introduc două valori independente.
Dat:
¯¯¯¯¯¯¯¯
Valoarea procentuală W = −120
Factor de creștere q = 95% = 0.95 = 19/20
Rezultate:
¯¯¯¯¯¯¯¯¯¯
Valoare de bază G = 2400
Procent p% = −5% = −0.05 = −1/20
Valoare finală E = 2280
Numere zecimale în fracții
Programul convertește fracțiile zecimale periodice și finite în fracții.
Parte neperiodică: 1.20
Periodă: 045
___
1.20045 = 120/100 + 1/2220 = 533/444
Fracții în zecimale
Programul convertește fracțiile în fracții zecimale periodice și determină perioada și lungimea acesteia.
numărător : 533
numitor : 444
___
533/444 = 1.20045
Zecimala periodică începe cu
a 3-a cifră după virgula zecimală
și are lungimea de 3 cifre.
Binomiale de gradul n
Formula binomială (a + b)2 = a2 + 2ab + b2 este cu siguranță una dintre cele mai cunoscute formule din matematica școlară.
Programul calculează cazul mai general (a·x + b·y)n.
(2·x - 3·y)7 = +128·x7
−1344·x6 · y
+6048·x5 · y2
−15120·x4 · y3
+22680·x3 · y4
−20412·x2 · y5
+10206·x · y6
−2187·y7
Ecuații de gradul 4
Programul determină soluțiile reale ale unei ecuații de gradul 4 sau mai mic. Pentru ecuațiile de grad mai mare nu există o metodă algebrică de rezolvare, în afară de calculele aproximative (rădăcini în programul Calculul funcțiilor arbitrare).
x4 + 2·x3 - 3·x2 + 5·x - 5 = 0 <=> (x - 1)·(x3 + 3·x2 + 5) = 0
L = {-3,42599; 1}
Ecuații diofantice
Programul calculează soluțiile întregi ale ecuației a·x - b = m·y cu m>0.
Aceasta permite, de exemplu, determinarea punctelor întregi pe o linie dreaptă.
7·x − 3·y − 5 = 0 ; x,y întregi
L = { ( 2 + 3t | 3 + 7t ) }
Triple pitagoreice
Triplele pitagoreice sunt soluțiile întregi (x, y, z) ale ecuației x2 + y2 = z2, care se aplică laturilor triunghiurilor dreptunghice.
Pentru x, y, z între 100 și 400 obținem:
( 119, 120, 169 ) ( 104, 153, 185 ) ( 133, 156, 205 ) ( 105, 208, 233 ) ( 140, 171, 221 ) ( 115, 252, 277 ) ( 120, 209, 241 ) ( 161, 240, 289 ) ( 160, 231, 281 ) ( 207, 224, 305 ) ( 175, 288, 337 ) ( 135, 352, 377 ) ( 136, 273, 305 ) ( 204, 253, 325 ) ( 225, 272, 353 ) ( 189, 340, 389 ) ( 180, 299, 349 ) ( 252, 275, 373 ) ( 152, 345, 377 ) ( 228, 325, 397 )
Calculatoare
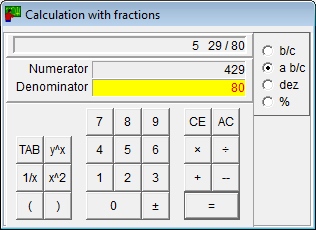
- Calculatorul pentru fracții poate efectua cele patru operații aritmetice de bază și poate ridica fracțiile la putere.
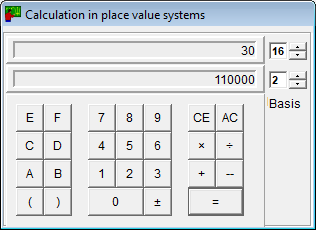
- Calculatorul pentru sisteme de valori poziționale funcționează cu orice bază între 2 și 16.
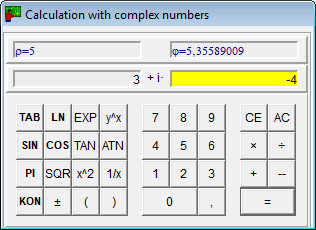
- Pe lângă funcțiile obișnuite, calculatorul pentru numere complexe calculează și conjugatele complexe ale unui număr.
Calcul cu numere mari (nou în versiunea 9.0 din aprilie 2021)
Calculul se bazează pe numere întregi cu maximum 10.000 de cifre.
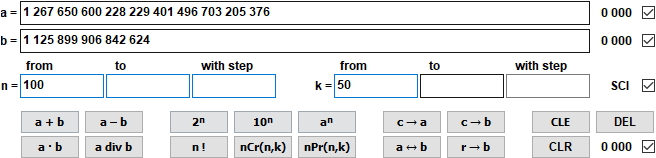
1 267 650 600 228 229 401 496 703 205 376 div 1 125 899 906 842 624 = 1 125 899 906 842 624 Rest 0 = 1,13 · 10^15 Rest 0 nCr(100,50) = 100 891 344 545 564 193 334 812 497 256 = 1,01 · 10^29
