MatheAss 10.0 − Geometrie 2D

Triunghiuri dreptunghice

Dacă sunt date două proprietăți ale unui triunghi dreptunghic, programul calculează celelalte.

Dat:
¯¯¯¯¯¯
Segment pe ipotenuză  p = 1,8
                  Aria  A = 6 
 
Rezultate :
¯¯¯¯¯¯¯
              Cateta a = 3
              Cateta b = 4
       Ipotenuza c = 5
                Unghiul  α = 36,869898°
                Unghiul  β = 53,130102°  
Segment pe ipotenuză  q = 3,2
             Înălțimea  h = 2,4

Triunghiuri după trei elemente

Dacă sunt date trei proprietăți exterioare (laturi sau unghiuri) ale unui triunghi, programul calculează laturile, unghiurile, înălțimile, medianele și bisectoarele, perimetrul și aria, precum și centrele și razele cercului înscris și ale cercului circumscris.

. 
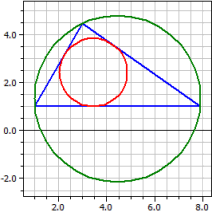
Dat:  a=6, b=4 și α=60°

   Vârfuri : A(1|1)         B(7,899|1)     C(3|4,4641)    
      Laturi : 6                  4                    6,89898        
    Unghiuri : 60°               35,2644°       84,7356°       
 Înălțimi : 3,98313       5,97469         3,4641         
 Mediane : 4,77472       6,148             3,75513        
   Bisectoare : 4,38551       6,11664         3,5464         

Cercul circumscris: M(4,44949|1,31784)       ru = 3,4641
    Cercul înscris : O(3,44949|2,41421)       r i = 1,41421

       Aria : A = 11,9494   Perimetru : u = 16,899
Triunghi

Triunghiuri din trei puncte

Din coordonatele a trei vârfuri, programul calculează toate proprietățile exterioare și interioare (vezi Triunghiuri după trei elemente ).

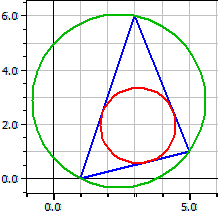
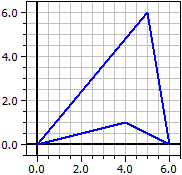
  Vârfuri :  A(1|0)          B(5|1)           C(3|6)         
     Laturi :  5,38516        6,32456       4,12311        
    Unghiuri :  57,5288°      82,2348°     40,2364°       
 Înălțimi :  4,0853         3,47851        5,33578        
 Mediane :  4,60977       3,60555        5,5            
   Bisectoare :  4,37592       3,51849        5,46225        

Cercul circumscris:  M(2,40909|2,86364)       ru = 3,19154
    Cercul înscris :  O(3,11866|1,96195)       r i = 1,38952

         Aria :  A = 11           Perimetru : u = 15,8328

Linii speciale într-un triunghi (Nou în versiunea 9.0)

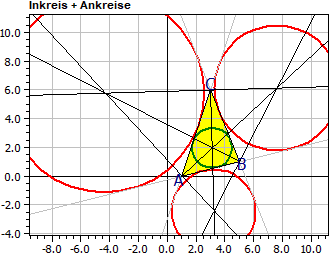
Programul determină ecuațiile mediatoarelor perpendiculare, medianelor, bisectoarelor și înălțimilor unui triunghi. În plus, centrele și razele cercului circumscris, cercului înscris, celor trei cercuri exinscrise și cercului celor nouă puncte (din martie 2025).

. 
Dat:
¯¯¯¯¯¯
   Vârfuri:    A(1|0)   B(5|1)   C(3|6)
 
Rezultate:
¯¯¯¯¯¯¯
       Laturi:   a :  5·x + 2·y = 27
                    b :  3·x - y = 3
                    c :  x - 4·y = 1
 
   Cercul înscris:    Mi(3,119|1,962)         r i = 1,390  
 
   Cercuri exinscrise: Ma(7,626|6,136)       ra = 4,346
                   Mb(-4,356|5,784)      rb = 6,910
                   Mc(3,248|-2,427)      rc = 2,900

Poligoane regulate

Dacă este dat numărul de colțuri și una dintre următoarele mărimi, programul calculează celelalte.
Latura a, raza cercului înscris ri, raza cercului circumscris rc, perimetrul u  sau aria A. 

Dat:
¯¯¯¯¯¯ 
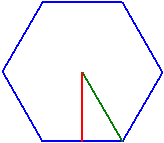
       Vârfuri  n = 6
Cercul circumscris rc = 1
 
Rezultate:
¯¯¯¯¯¯¯ 
           Latura  a = 1
        Cercul înscris ri = 0,8660254
   Perimetru  p = 6
           Aria  A = 2,5980762

Poligoane arbitrare

Din coordonatele vârfurilor unui poligon, programul calculează aria, perimetrul, centrul de greutate al vârfurilor și centrul de greutate al ariei. 

Vârfuri:          Aria  A = 18
 A(0|0)     
 B(4|1)     Perimetru  p = 22,032567
 C(6|0)     
 D(5|7)     Centrul de greutate al vârfurilor:
                CV(3,75|2)
            
                Centrul de greutate al ariei:
                CA(3,72222|2,66667)

Transformări ale poligoanelor (revizuit în versiunea 9.0)

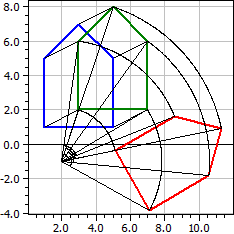
Programul permite aplicarea unei concatenări de transformări asupra unui poligon. Se poate alege dintre translație, reflexie axială, reflexie punctuală, rotație, omotetie și forfecare. 

Poligon inițial
A(1|1), B(5|1), C(5|5), D(3|7), E(1|5), 

1. Translație: dx=2, dy=1  ☑
A(3|2), B(7|2), C(7|6), D(5|8), E(3|6), 

2. Rotație: Z(2|-1), α=−60° ☑
A(5,0981|-0,36603), B(7,0981|-3,8301),
C(10,562|-1,8301), D(11,294|0,90192),
E(8,5622|1,634),

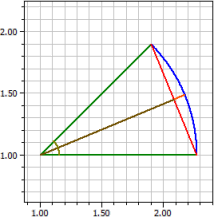
Părți de cerc

Dacă sunt date două dintre următoarele mărimi, programul calculează celelalte. 

Dat:
¯¯¯¯¯¯ 
                 Arc b = 1
             Unghi α = 45°

Rezultate:  
¯¯¯¯¯¯¯ 
           Raza r = 1,2732395
            Coarda s = 0,97449536
       Sector A1 = 0,63661977
       Distanța d = 1,17632
 Săgeata h = 0,096919589
    Segment A2 = 0,063460604

             Aria A = 5,0929582
     Perimetru p = 8

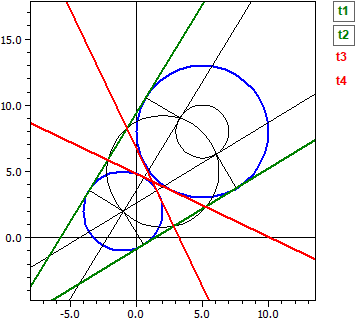
Tangente la cercuri (Nou în versiunea 9.0 din februarie 2021)

Se calculează ecuaþiile următoarelor tangente:

  • Tangenta la un cerc k într-un punct B
  • Tangentele la un cerc k printr-un punct P exterior cercului
  • Tangentele la un cerc k paralele cu o dreaptă g
  • Tangentele la două cercuri k1 şi k2
Dat:
¯¯¯¯¯
  k1 : M(5|8) ,    r=5
  k2 : M(-1|2) ,   r=3

Tangente exterioare
¯¯¯¯¯¯¯¯¯¯¯¯
  t1: -4,2923·x + 7,04104·y = -6,36427
  t2: -7,04104·x + 4,29230·y = 40,3643

Tangente interioare
¯¯¯¯¯¯¯¯¯¯¯¯
  t3: 1,21895·x + 2,55228·y = 12,3709
  t4: -2,55228·x - 1,21895·y = -8,3709

Intersecþii în plan

Programul calculează intersecþiile dintre drepte şi cercuri

Două drepte

g : x + y = 0
h : x - y = 5

Punct de intersecþie : S(2,5|-2,5)

Unghi de intersecþie : 90°

Distanþe faþă de origine :
  d(g,O) = 0
  d(h,O) = 3,5355339

Dreaptă şi cerc

Cerc şi dreaptă :
¯¯¯¯¯¯¯¯¯¯¯¯¯
  k : M(5|0)   r = 5
  g : x + y = 0

Puncte de intersecþie :      
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  S1(5|-5)
  S2(0|0)

Două cercuri

Sunt date cercurile :         
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 
k1 : M1(5|5) r1 = 5
k2 : M2(0|0) r2 = 5

Puncte de intersecþie :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 
S1(5|0)   S2(0|5)

Dreapta de legătură :
¯¯¯¯¯¯¯¯¯¯¯¯¯
 x + y = 5