MatheAss - Stocastică
Statistici
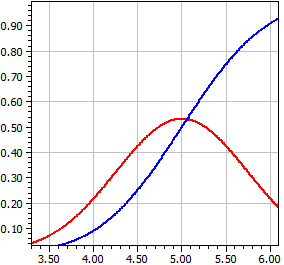
Pentru o listă de date, sunt determinate media (media aritmetică), valoarea centrală (mediana), varianța și abaterea standard. În plus, distribuția este afișată sub formă de histogramă și box plot.
Date:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8
Număr de date n = 21
Maxim max = 11
Minim min = 1
Media x = 7,7142857
Mediana c = 8
Varianță s² = 6,1142857
Abatere standard s = 2,4727082
Regresie
Cu această rutină, se poate efectua ajustarea unei curbe pentru o serie de măsurători. Se poate alege între următoarele ajustări și, dacă este necesar, se pot deplasa sau scala toate punctele în direcția x sau y.
Regresie proporțională ( y = a·x )
Regresie liniară ( y = a·x + b )
Regresie polinomială de ordin n ( y = a0 + ... + an·xn )
Regresie geometrică ( y = a·xb )
Regresie exponențială ( y = a·bx )
Regresie logaritmică ( y = a + b·ln(x) )
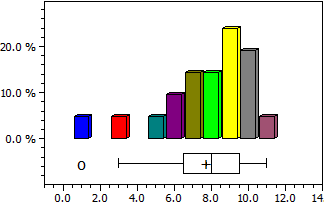
Regresie polinomială
y = - 6,9152542
+ 4,7189266·x
- 0,43361582·x2
Coeficient de determinare = 0,98338318
Coeficient de corelație = 0,99165679
Abatere standard = 0,46028731
Regresie logistică
(Nou în versiunea 9.0)
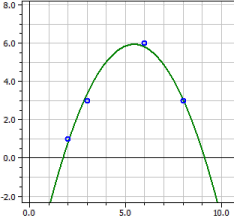
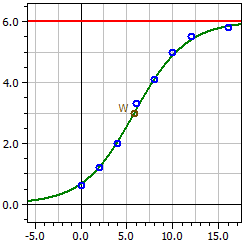
Programul determină pentru o serie de măsurători o ajustare de curbă la funcția logistică
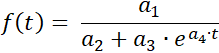
cu parametrii a1 = ƒ(0)· S , a2 = ƒ(0) , a3 = S - ƒ(0) ,
și a4 = -k· S și limita de saturație S.
Date din: "hopfenwachstum.csv"
Limită de saturație: 6
Valoare ascunsă: 1
4,0189
ƒ(x) = ————————————————
0,66981 + 5,3302 · e^(-0,35622·t)
Punct de inflexiune W(5,8226/3)
Rata maximă de creștere ƒ'(xw) = 0,53433
8 valori
Coeficient de determinare = 0,99383916
Coeficient de corelație = 0,99691482
Abatere standard = 0,16172584
Combinatorică
Numărul de posibilități de a selecta k din n elemente este calculat în funcție de faptul dacă ordinea contează sau nu și dacă sunt permise sau nu repetițiile.
n = 49 k = 6 Aranjamente fără repetiție = 10 068 347 520 Aranjamente cu repetiții = 13 841 287 201 Combinații fără repetiție = 13 983 816 Combinații cu repetiții = 25 827 165 Permutări ale lui k : k! = 720
Distribuția binomială
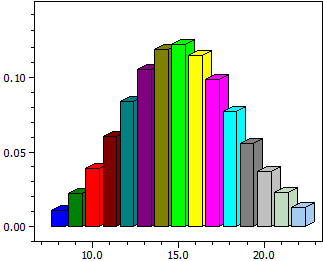
Calculat pentru o variabilă aleatoare X distribuită b(k;n;p) la n fix și p fix
- un diagramă cu bare a probabilităților P(X=k)
- valorile lor numerice într-un interval [k-min;k-max]
- probabilitatea P( k-min < = X <= k-max)
n = 50 p = 0,3
k P(X=k) P(0<=X<=k)
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
8 0,01098914 0,01825335
9 0,02197829 0,04023163
10 0,03861899 0,07885062
11 0,06018544 0,13903606
12 0,08382972 0,22286578
13 0,10501745 0,32788324
14 0,11894834 0,44683157
15 0,12234686 0,56917844
16 0,11470018 0,68387862
17 0,09831444 0,78219306
18 0,07724706 0,85944012
19 0,05575728 0,91519740
20 0,03703876 0,95223616
21 0,02267679 0,97491296
22 0,01281092 0,98772387
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
P(8<=k<=22) = 0,98045967
Distribuția hipergeometrică
Se fac calcule pentru o variabilă aleatoare X distribuită h(k; n; m; r) cu n, m și r fixe, un grafic cu bare și un tabel de valori pentru probabilitățile P(X=k).
Distribuția normală
Se efectuează calcule pentru o variabilă aleatoare X distribuită N(μ, σ2) cu o valoare așteptată μ și varianță σ2, funcția de densitate ƒ(x) și funcția de distribuție Φ(x), adică integrala peste ƒ(x).
μ = 5 , σ = .75
x ƒ(x) Φ(x)
¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
2 0,00017844 0,00003167
2,33333333 0,00095649 0,00018859
2,66666666 0,00420802 0,00093192
2,99999999 0,01519465 0,00383038
3,33333332 0,04503153 0,01313415
3,66666665 0,10953585 0,03772017
3,99999998 0,21868009 0,09121120
4,33333331 0,35832381 0,18703139
4,66666664 0,48189843 0,32836063
4,99999997 0,53192304 0,49999998
5,3333333 0,48189845 0,67163934
5,66666663 0,35832383 0,81296859
5,99999996 0,21868012 0,90878878
6,33333329 0,10953586 0,96227982
6,66666662 0,04503154 0,98686585
6,99999995 0,01519465 0,99616962
7,33333328 0,00420802 0,99906808
7,66666661 0,00095649 0,99981141
7,99999994 0,00017844 0,99996833
