MatheAss 10.0 - Algebră Liniară

Sisteme de ecuații liniare

Programul determină vectorul soluție dintr-un sistem de ecuații liniare cu n ecuații și n necunoscute.

Exemplu: Căutarea unei parabole prin punctele P (1|3), Q (2|1) și R (4|9) conduce la sistemul de ecuații

  1·x1 + 1·x2 + 1·x3 = 3
  4·x1 + 2·x2 + 1·x3 = 1
 16·x1 + 4·x2 + 1·x3 = 9   
            
 L = (2; -8; 9)

Deci parabola are ecuația y = 2x ² - 8x + 9.

Exemplu cu spațiu soluție bidimensional:

  0·x1 + 0·x2 + 2·x3 - 1·x4  =  1
  1·x1 + 1·x2 + 1·x3 + 1·x4  =  4
  2·x1 + 2·x2 - 4·x3 + 5·x4  =  5
  1·x1 + 1·x2 - 7·x3 + 5·x4  =  0

  L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }

Optimizare liniară (din februarie 2022)

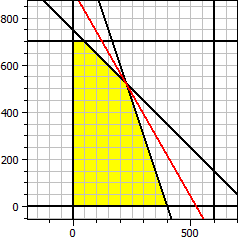
Programul determină soluția optimă pentru o funcție obiectiv cu două variabile și inegalități liniare ca restricții.

Funcția obiectiv:
  ƒ(x,y) = 140·x + 80·y → Maxim

Restricții:
  x ≥ 0
  y ≥ 0
  x ≤ 600
  y ≤ 700
  x + y ≤ 750
  3·x + y ≤ 1200

Maxim:
  x = 225   y = 525
  ƒ(x,y) = 73500

Programul determină combinația liniară a unui vector din trei vectori dați. Rutina este de asemenea potrivită pentru verificarea independenței liniare a trei vectori în spațiu, adică dacă aceștia se află într-un plan.


    ⎧ 1 ⎫     ⎧ 1 ⎫     ⎧ 1 ⎫   ⎧ 2 ⎫
  a·⎪ 0 ⎪ + b·⎪ 1 ⎪ + c·⎪ 1 ⎪ = ⎪ 3 ⎪
    ⎩ 0 ⎭     ⎩ 0 ⎭     ⎩ 1 ⎭   ⎩ 4 ⎭

 Soluție:
     a = -1  b = -1  c = 4

Produs scalar

Programul calculează produsul scalar a două vectori, lungimea celor doi vectori și unghiul inclus.


   ->  ⎧ 1 ⎫     ->  ⎧ 5 ⎫
   a = ⎪ 3 ⎪     b = ⎪ 0 ⎪
       ⎩ 1 ⎭         ⎩ 3 ⎭
           
Produsul scalar al vectorilor  = 8

Lungimea primului vector       = √11 = 3.32

Lungimea celui de-al doilea    = √34 = 5.83

Unghiul inclus                 α = 65.56°

Produs vectorial

Programul calculează produsul vectorial și modulul acestuia pentru doi vectori. Produsul vectorial este perpendicular pe paralelogramul generat de aceștia, iar modulul său este egal cu aria paralelogramului.


     ->  ⎧ 1 ⎫     ->  ⎧ 7 ⎫
     a = ⎪ 2 ⎪     b = ⎪ 1 ⎪
         ⎩ 3 ⎭         ⎩ 4 ⎭

 ->  ->  ⎧  5 ⎫    ->  ->  
 a x b = ⎪ 17 ⎪   |a x b|= √483 = 21,977261
         ⎩-13 ⎭

Produs triplu

Programul calculează produsul mixt pentru trei vectori. Modulul său indică volumul paralelipipedului (cuboidului) generat de cei trei vectori.


->  ⎧ 2 ⎫     ->  ⎧ 2 ⎫    ->  ⎧ 3 ⎫
a = ⎪ 3 ⎪     b = ⎪-1 ⎪    c = ⎪ 9 ⎪
    ⎩ 5 ⎭         ⎩ 7 ⎭        ⎩ 2 ⎭

  ->  ->    ->  
( a x b ) · c = 26

Inversarea matricii

Programul calculează determinantul, rangul și matricea inversă pentru o matrice pătratică de ordin n.

Matrice :        
¯¯¯¯¯¯¯¯
  ⎧ 1  0  2 ⎫
  ⎪ 0  1  0 ⎪
  ⎩ 3  0  1 ⎭

Matrice inversă :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧-0,2  0  0,4 ⎫
  ⎪   0  1    0 ⎪
  ⎩ 0,6  0 -0,2 ⎭

Ordin = 3,  Rang = 3,  Determinant = -5

Matrice pseudoinversă

Dacă coloanele unei matrici A sunt liniar independente, atunci A ^T A este inversabilă și pseudoinversa se obține cu formula următoare:

A⁺ = ( A^T· A )^-1· A^T

A⁺ este o inversă stângă a lui A, adică se aplică relația: A⁺ * A = E.

Matrice A
¯¯¯¯¯¯¯¯
  ⎧ 1  1  1  1 ⎫
  ⎩ 5  7  7  9 ⎭

A^T· A
¯¯¯¯
  ⎧ 26  36  36  46 ⎫
  ⎪ 36  50  50  64 ⎪
  ⎪ 36  50  50  64 ⎪
  ⎩ 46  64  64  82 ⎭

A^T· A nu este inversabilă

A · A^T
¯¯¯¯¯¯
  ⎧  4   28 ⎫
  ⎩ 28  204 ⎭

( A · A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧ 6,375 -0,875 ⎫
  ⎩-0,875  0,125 ⎭

Inversă dreaptă:  A^T·( A·A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧    2 -0,25 ⎫
  ⎪ 0,25     0 ⎪
  ⎪ 0,25     0 ⎪
  ⎩ -1,5  0,25 ⎭

Înmulțirea matricilor

Programul calculează matricea produs pentru două matrici.

1. Matrice :     
¯¯¯¯¯¯¯¯¯¯
  ⎧ 1  0  2 ⎫
  ⎩ 0  1  0 ⎭

2. Matrice :     
¯¯¯¯¯¯¯¯¯¯
  ⎧-0,2  0  0,4  1 ⎫
  ⎪   0  1    0  1 ⎪
  ⎩ 0,6  0 -0,2  1 ⎭

Matricea produs:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧ 1  0  0  3 ⎫
  ⎩ 0  1  0  1 ⎭

MatheAss 10.0 - Algebră Liniară

A+ = ( AT· A )-1· AT

A⁺ = ( A^T· A )^-1· A^T