MatheAss 10.0 - Analiză
Șiruri și serii (Nou în versiunea 9.0 din mai 2021)
Programul determină primii n termeni ai unui șir (ai) și seria corespunzătoare (suma termenilor șirului) dacă sunt date primii termeni ai șirului și o funcție explicită ai=ƒ(i) sau o formulă de recurență ai=ƒ(a0, a1, ... , ai-1).
Șir ¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Serie ¯¯¯¯ ( Σ a[ i ] ) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
Împărțirea polinoamelor
Programul calculează produsul și câtul a două polinoame.
Primul polinom: 3·x4 - 2 x + 1
Al doilea polinom: 2·x + 5
Produs: 6·x5 + 15·x4 - 4·x2 - 8·x + 5
Cât: 3/2·x3 - 15/4·x2 + 75/8·x - 391/16
Rest: 1971/16
Factorizarea polinoamelor (Nou în versiunea 9.0)
Programul calculează rădăcinile raționale și descompunerea în factori liniari a unui polinom.
p(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 + x - 9
= (1/9)·(9·x5 - 81·x4 - 82·x3 + 738·x2 + 9·x - 81)
= (1/9)·(3·x - 1)·(3·x + 1)·(x - 9)·(x - 3)·(x + 3)
Rădăcini raționale: 1/3, -1/3, 9, 3, -3
Transformarea polinoamelor (Nou în versiunea 9.0)
O funcție polinomială ƒ(x) poate fi translatată sau scalată în direcția x și y.
ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Translatat cu dx = -2, dy = 0 ƒ(x + 2) = - 1/4 ·x4 + 6 ·x2 + 1
CMMDC și CMMMC ale polinoamelor (Nou în versiunea 9.0 din februarie 2021)
Programul calculează cel mai mare divizor comun (CMMDC) și cel mai mic multiplu comun (CMMMC) a două polinoame p1(x) și p2(x).
p1(x) = 4·x6 - 2·x5 - 6·x4- 18·x3 - 2·x2 + 24·x + 8 p2(x) = 10·x4- 14·x3 - 22·x2 + 14·x + 12 CMMDC(p1,p2) = x2 - x - 2 CMMMC(p1,p2) = 40·x8 - 36·x7 - 76·x6 - 144·x5 + 88·x4+ 356·x3 - 4·x2 - 176·x - 48
Plotarea funcțiilor
Până la zece funcții pot fi desenate simultan într-un sistem de coordonate. Sunt permise și legături sau derivate ale funcțiilor deja definite.
Dacă ƒ1(x) = sin(x) și ƒ2(x) = 3*sqrt(x), atunci ƒ3(x) = 2*y1^2-y2 substituie ƒ3(x) = 2*sin(x)^2-3*sqrt(x) ƒ4(x) = f2(y1) substituie ƒ4(x) = 3*sqrt(sin(x)) ƒ5(x) = y2' substituie ƒ5(x) = 3/(2*sqrt(x))
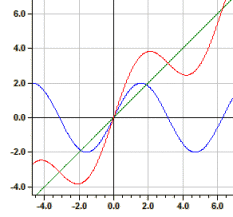
Exemplu: ƒ1(x)=sin(x), ƒ2(x)=x și ƒ3(x)=y1+y2
Funcții definite pe segmente
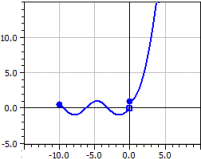
Este desenată o funcție definită pe segmente, care este dată de până la nouă subfuncții. Pentru fiecare subfuncție se introduc domeniul de definiție, tipul intervalului și culoarea. Este de asemenea posibilă determinarea dacă punctele de frontieră sunt desenate sau nu.
Exemplu:
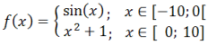
Curbe parametrice
Cu acest program pot fi desenate curbe care nu sunt date printr-un termen funcțional explicit, ci prin două funcții pentru deviația orizontală și verticală.
Exemplu: Figuri Lissajou
x(k) = sin(3*k)
y(k) = cos(5*k)
k de la -Pi la Pi
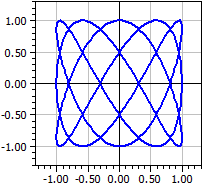
Figurile Lissajou sunt obținute atunci când două tensiuni alternative de frecvențe diferite sunt aplicate la un osciloscop.
Figurile Lissajou sunt obținute atunci când două tensiuni alternative cu frecvențe diferite sunt aplicate la un osciloscop.
Familii de curbe
Programul desenează graficele oricărei funcții care conține un parametru k. Valorile pentru k pot fi listate sau determinate prin valoare inițială, valoare finală și pas.
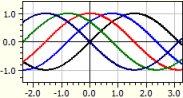
ƒ(x,k) = sin(x+k)
k de la -2 la 2 cu pas Pi/4
Analiza funcțiilor polinomiale
(Nou în versiunea 9.0)
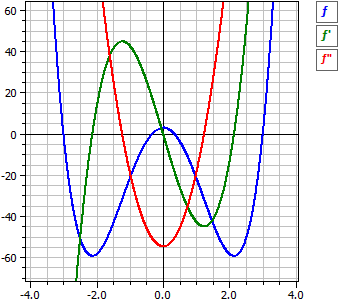
Programul efectuează discuția curbei pentru o funcție polinomială. Astfel, sunt determinate derivatele și funcția primitivă, funcția este analizată pentru rădăcini raționale, extreme, puncte de inflexiune și simetrie.
Funcție:
¯¯¯¯¯¯¯¯
ƒ(x) = 3·x4 - 82/3·x2 + 3
= 1/3·(9·x4 - 82·x2 + 9)
= 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)
Derivate:
¯¯¯¯¯¯¯¯¯¯
ƒ'(x) = 12·x3 - 164/3·x
ƒ"(x) = 36·x2 - 164/3
ƒ'"(x) = 72·x
Funcția primitivă:
¯¯¯¯¯¯¯¯¯¯¯
F(x) = 3/5·x5 - 82/9·x3 + 3·x + c
.
.
.
Analiza funcțiilor raționale
(Nou în versiunea 9.0)
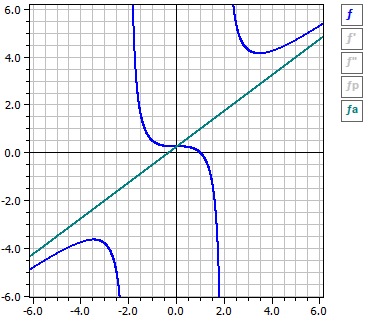
Programul efectuează discuția curbei pentru o funcție rațională. Astfel, sunt determinate derivatele, discontinuitățile și continuarea continuă. Funcția este analizată pentru zerouri, extreme, puncte de inflexiune și comportamentul pentru |x|→ ∞.
Funcție :
¯¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Singularități:
¯¯¯¯¯¯¯¯¯¯¯
x = 2 Pol cu schimbare de semn
x = -2 Pol cu schimbare de semn
Derivate:
¯¯¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = ————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ———————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
.
.
.
Analiza funcțiilor arbitrare
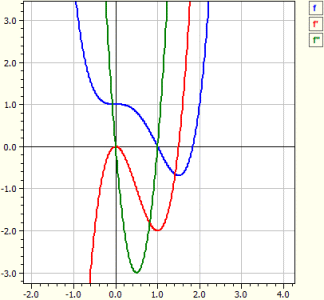
Programul efectuează discuția curbei pentru orice funcție. Astfel, sunt determinate derivatele, funcția este analizată pentru zerouri, extreme și puncte de inflexiune, se desenează graficele lui ƒ, ƒ' și ƒ", și se afișează un tabel de valori.
Funcție: ‾‾‾‾‾‾‾‾‾‾‾‾ ƒ(x) = x^4-2*x^3+1 Analiză în intervalul de la -10 la 10 Derivate: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ'(x) = 4*x^3-6*x^2 ƒ"(x) = 12*x^2-12*x Zerouri: ‾‾‾‾‾‾‾‾ N1(1|0) m = - 2 N2(1,83929|0) m = + 4,5912 Extreme: ‾‾‾‾‾‾‾‾‾‾‾‾‾ T1(1,5|-0,6875) m = 0 Puncte de inflexiune: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ W1(0|1) m = + 0 W2(1|0) m = - 2
Iterația Newton
Iterația Newton este o metodă de aproximare pentru calcularea unei rădăcini a lui ƒ(x). Dacă se introduce o valoare inițială x0 suficient de apropiată de rădăcina dorită, următoarea aproximare este intersecția tangentei la graficul lui f în punctul
ƒ(x) = x-cos(x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
Calculul integral (din februarie 2021 cu lungimi de arc)
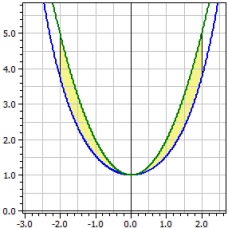
Conținuturile orientate și absolute ale suprafeței dintre două curbe de funcție sunt calculate într-un interval dorit [a; b].
În plus, se calculează momentele de torsiune pentru rotație, corpurile de rotație și lungimile de arc în interval.
ƒ1(x) = cosh(x) ƒ2(x) = x^2+1 Limitele integrării de la -2 la 2 Conținut orientat : A1 = -2,07961 Conținut absolut : A2 = 2,07961 Lungimi de arc : L1[a;b] = 7,254 L2[a,b] = 9,294
Dezvoltarea seriilor
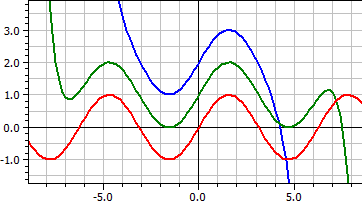
O funcție dată sub formă de serie este desenată, iar dezvoltările seriilor pentru diferite intervale de parametri pot fi comparate și deplasate pe direcția y pentru o diferențiere mai bună.
Cei 16 termeni ai seriei Taylor pentru funcția sinus. . ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) , k = 4, 8 și 16
Funcții de suprafață
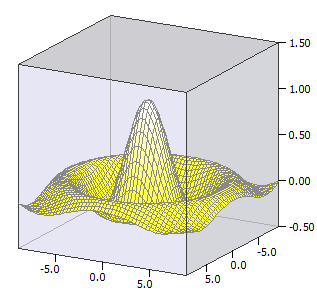
O funcție de suprafață ƒ(x,y), adică diagrama tridimensională a unei funcții cu două variabile, este desenată.
Exemplu:
ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)
-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5
