MatheAss 10.0 − Geometrie 3D
Sisteme de coordonate
Cu acest program, coordonatele carteziene tridimensionale pot fi convertite în coordonate sferice sau coordonate cilindrice şi invers.
cartezian polar cilindric x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
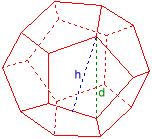
 Corpurile platonice
Corpurile platonice
Programul calculează cele cinci corpuri platonice: tetraedru, hexaedru, octaedru, dodecaedru şi icosaedru dacă sunt date lungimea muchiei, înălþimea feþei, înălþimea spaþiului, raza cercului înscris, raza cercului circumscris, volumul sau suprafaþa.
Exemplu: Dodecaedru
Dat:
¯¯¯¯¯¯
Diagonala feþei d = 2
Rezultate:
¯¯¯¯¯¯¯
Muchie a = 1,236068
Înălþimea feþei h = 1,902113
Raza cerc. circumscris rc = 1,7320508
Raza cerc. înscris ri = 1,3763819
Volum V = 14,472136
Suprafaþă S = 31,543867
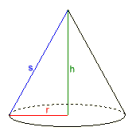
 Alte corpuri
Alte corpuri
Programul calculează toate mărimile unui prism regulat, ale unui cilindru circular drept, ale unei piramide regulate, ale unui con circular drept sau ale unei sfere dacă sunt date două dintre acestea.
Exemplu: Con circular
Dat:
¯¯¯¯¯¯
Volum V = 1
Baza B = 1
Rezultate:
¯¯¯¯¯¯¯
Raza r = 0,56418958
Înălþimea h = 3
Apotema s = 3,0525907
Suprafaþa laterală L = 5,4105761
Suprafaþa S = 6,4105761
Dreaptă prin 2 puncte
Dreaptă prin A(1|1|1), B(2|5|6)
Reprezentare parametrică
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
x = ⎪ 1 ⎪ + t·⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 5 ⎭
Distanþa faþă de origine
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 0,78679579
Poziþia faþă de planul xy
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Proiecþie : 4·x - y = 3
Punct inters.: S1(0,8|0,2|0)
Unghi inters.: 50,490288°
Poziþia faþă de planul yz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Proiecþie : 5·y - 4·z = 1
Punct inters.: S2(0|-3|-4)
Unghi inters.: 8,8763951°
Poziþia faþă de planul xz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Proiecþie : 5·x - z = 4
Punct inters.: S3(0,75|0|-0,25)
Unghi inters.: 38,112927°
Plan prin 3 puncte
Plan prin punctele:
A(1|2|3), B(2|3|3), C(1|0|1)
Formă punct-pantă:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪+r·⎪ 1 ⎪+s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
Ecuaþia în coordonate:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Distanþa faþă de origine:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Puncte de intersec.:
¯¯¯¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)
Sferă prin 4 puncte
Sferă prin punctele:
A(1|0|0), B(0|2|0),
C(0|0|3), D(1|0|1)
Formă normală:
¯¯¯¯¯¯¯¯¯¯¯¯
⎧ -> ⎧-2,5 ⎫ ⎫2
K: ⎪ x - ⎪-0,5 ⎪ ⎪= 12,75
⎩ ⎩ 0,5 ⎭ ⎭
Centru şi rază:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-2,5|-0,5|0,5)
r = 3,5707142
 Intersecþii în spaþiu
Intersecþii în spaþiu
Programul calculează secþiunile dintre drepte, plane şi sfere.
Două drepte
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Punct de intersec.: S(5|5|5)
Unghi de intersec.: 60°
Distanþe faþă de origine :
d(O,g)=5 d(O,h)=5
Plan şi dreaptă
Plan E :
¯¯¯¯¯¯¯¯¯
E : x + y + z = 5
Dreaptă g :
¯¯¯¯¯¯¯¯
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Punct de intersec.:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
S(5|0|0)
Unghi de intersec.:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
alpha = 54,73561°
Sferă şi dreaptă
Sferă :
¯¯¯¯¯¯¯¯
K : M(5|5|5) , r = 5
Dreaptă :
¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Puncte de intersec. :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
S1(2,81867|1,81867|1,81867)
S2(8,51467|7,51467|7,51467)
Lungimea coardei :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
s = 9,8657657
Două plane
Sunt date cele două plane:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1 : 5·x - 2·y = 5
E2 : 2·x - y + 5·z = 8
Dreapta de intersec.:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧-11 ⎫ ⎧ 10 ⎫
g : x = ⎪-30 ⎪ + r·⎪ 25 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Distanþa faþă de origine:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,5057283
Unghi de intersec.:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
alpha = 65,993637°
Două sfere
Sunt date cele două sfere: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ K1 : M1(3|3|3) , r1 = 3 K2 : M2(1|1|1) , r2 = 3 Cercul de intersec.: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2), r = 2,4494897 Planul de intersec. : ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ E : x + y + z = 6
Sferă şi plan
Plan :
¯¯¯¯¯¯
E : 5·x - 4·y + 5·z = -3
Sferă :
¯¯¯¯¯¯¯¯
⎧ -> ⎧ 1 ⎫⎫2
K : ⎪ x - ⎪ 2 ⎪⎪ = 16
⎩ ⎩ 3 ⎭⎭
Cercul de intersec. :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(1|1|1), r = 2
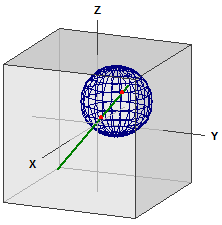
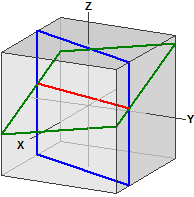
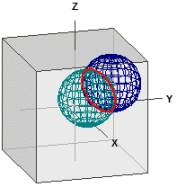
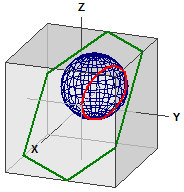
 Distanþe pe sferă
(Nou în versiunea 9.0 din decembrie 2021)
Distanþe pe sferă
(Nou în versiunea 9.0 din decembrie 2021)
Distanþa dintre două puncte pe o sferă este calculată. Programul este de asemenea potrivit pentru conversia gradelor zecimale în grade, minute şi secunde (dms) şi invers.
GPS zecimal ¯¯¯¯¯¯¯¯¯¯¯ Berlin : 52.523403, 13.4114 New York : 40.714268, -74.005974 GPS dms ¯¯¯¯¯¯ Berlin : 52° 31' 24.2508" N, 13° 24' 41.0400" E New York : 40° 42' 51.3648" N, 74° 0' 21.5064" W . . . Distanþă ¯¯¯¯¯¯¯¯ d = r · α [rad] = 6385,112

