MatheAss 10.0 − Analyysi
Jonot ja sarjat (Uutta versiossa 9.0 toukokuusta 2021)
Ohjelma määrittää jonon (ai) ensimmäiset n termiä ja siihen liittyvän sarjan (jonon termien summa), kun jonon ensimmäiset termit ja eksplisiittinen funktio ai=ƒ(i) tai rekursiokaava ai=ƒ(a0, a1, ... , ai-1) on annettu.
a[0]=1; a[1]=1; a[ i ] = a[i-1] + a[i-2]; n = 20 Jono ¯¯¯¯¯ ( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Sarja ¯¯¯¯¯ ( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
Polynomien jakaminen
Ohjelma laskee kahden polynomin tulon ja osamäärän.
1. Polynom: 3·x4 - 2·x + 1
2. Polynom: 2·x + 5
Tulo: 6·x5 + 15·x4 - 4·x2 - 8·x + 5
Osamäärä: 3/2·x3 - 15/4·x2 + 75/8·x - 391/16
Jäännös: 1971/16
Polynomien tekijäihinjaotus (Uutta versiossa 9.0)
Ohjelma laskee polynomin rationaaliset nollakohdat ja lineaarisen tekijäihinjaon.
p(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 + x - 9
= (1/9)·(9·x5 - 81·x4 - 82·x3 + 738·x2 + 9·x - 81)
= (1/9)·(3·x - 1)·(3·x + 1)·(x - 9)·(x - 3)·(x + 3)
Rationaaliset nollakohdat: 1/3, -1/3, 9, 3, -3
Polynomien muunnokset (Uutta versiossa 9.0)
Polynomifunktiota ƒ(x) voidaan siirtää x- ja y-suunnassa tai venyttää.
ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Siirto dx = -2 , dy = 0 ƒ(x + 2) = - 1/4·x4 + 6·x2 + 1
Polynomien syt ja ptk (Uutta versiossa 9.0 helmikuusta 2021)
Ohjelma laskee kahden polynomin p1(x) ja p2(x) suurimman yhteisen tekijän (syt) ja pienimmän yhteisen kertoimen (ptk).
p1(x) = 4·x6 - 2·x5 - 6·x4- 18·x3 - 2·x2 + 24·x + 8 p2(x) = 10·x4- 14·x3 - 22·x2 + 14·x + 12 syt(p1,p2) = x2 - x - 2 ptk(p1,p2) = 40·x8 - 36·x7 - 76·x6 - 144·x5 + 88·x4+ 356·x3 - 4·x2 - 176·x - 48
Funktiopiirturi 1
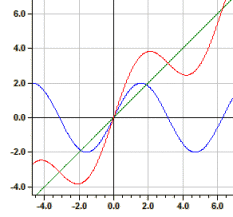
Voidaan piirtää jopa kymmenen funktiota samanaikaisesti yhteen koordinaatistoon. Sallittuja ovat myös yhdisteet ja jo määriteltyjen funktioiden derivaatat.
Olkoon ƒ1(x)=sin(x) ja ƒ2(x)=3*sqrt(x), silloin saadaan ƒ3(x)=2*y1^2-y2 ƒ3(x)=2*sin(x)^2-3*sqrt(x) ƒ4(x)=f2(y1) ƒ4(x)=3*sqrt(sin(x)) ƒ5(x)=y2' ƒ5(x)=3/(2*sqrt Esimerkki: ƒ1(x)=sin(x), ƒ2(x)=x ja ƒ3(x)=y1+y2
Funktiopiirturi 2
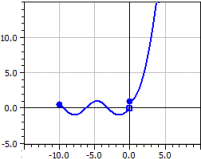
Piirretään osittain määritelty funktio, joka koostuu yhdeksästä osafunktiosta. Jokaiselle osafunktiolle annetaan määrittelyjoukko, intervallin tyyppi ja väri. Lisäksi voidaan määrittää, piirretäänkö rajapisteet vai ei.
Esimerkki:
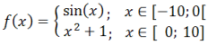
Parametrikäyrät
Tällä ohjelmalla voidaan piirtää käyriä, joita ei ole annettu eksplisiittisenä funktiona, vaan kahden funktion avulla horisontaaliselle ja vertikaaliselle poikkeamalle.
Esimerkki: Lissajous-kuviot
x(k) = sin(3*k)
y(k) = cos(5*k)
k väliltä -Pi ... Pi
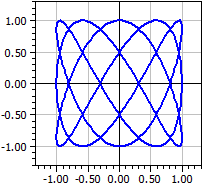
Lissajous-kuvioita saadaan, kun oskilloskooppiin kytketään kaksi eritaajuista vaihtojännettä.
Käyräperheet
Ohjelma piirtää minkä tahansa funktion kuvaajat, jotka sisältävät perusparametrin k. Arvot k:lle voidaan luetella tai määrittää alkuarvo, loppuarvo ja askelpituus.
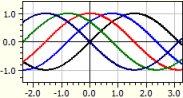
ƒ(x,k) = sin(x+k)
k väliltä -2 ... 2 askelpituudella Pi/4
Polynomifunktiot (Uutta versiossa 9.0)
Ohjelma suorittaa kokonaisrationaalisen funktion (polynomifunktion) käyräanalyysin. Se tarkoittaa, että määritetään derivaatat ja integraalifunktio, tutkitaan rationaaliset nollakohdat, ääriarvot, taitepisteet ja symmetria.
Funktio :
¯¯¯¯¯¯¯¯
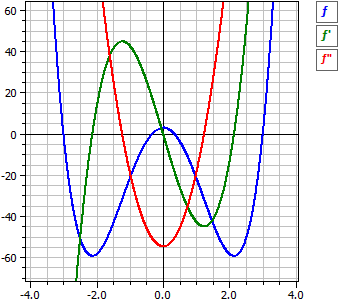
ƒ(x) = 3·x4 - 82/3·x2 + 3
= 1/3·(9·x4 - 82·x2 + 9)
= 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)
Derivaatat :
¯¯¯¯¯¯¯¯¯¯
ƒ'(x) = 12·x3 - 164/3·x
ƒ"(x) = 36·x2 - 164/3
ƒ'"(x) = 72·x
Integraalifunktio
¯¯¯¯¯¯¯¯¯¯¯¯
ƒ(x) = 3/5·x5 - 82/9·x3 + 3·x + c
.
.
.
Rationaaliset funktiot (Uutta versiossa 9.0)
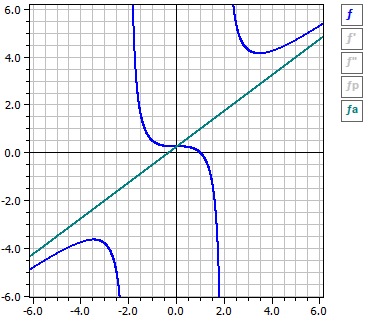
Ohjelma suorittaa (murtorationaalisen) funktion käyräanalyysin. Se tarkoittaa, että määritetään derivaatat, määrittelyaukot ja jatkuva jatke. Funktiota tutkitaan nollakohtien, ääriarvojen, taitepisteiden ja käytöksen suhteen, kun |x|→∞.
Funktio :
¯¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Määrittelyaukot
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x = 2 Napa etumerkinvaihdolla
x = -2 Napa etumerkinvaihdolla
Derivaatat :
¯¯¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = —————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ————————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
.
.
.
Käyräanalyysi
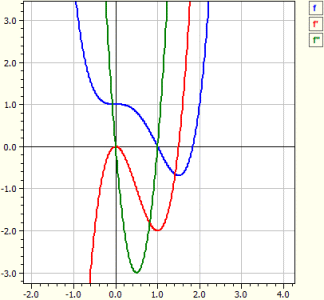
Ohjelma suorittaa minkä tahansa funktion käyräanalyysin. Se tarkoittaa, että määritetään derivaatat, tutkitaan nollakohdat, ääriarvot ja taitepisteet, piirretään ƒ, ƒ' ja ƒ" kuvaajat sekä tulostetaan arvotaulukko.
Funktio : ‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ(x) = x^4 - 2*x^3 + 1 Tutkimus alueella -10 ... 10 Derivaatat: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ'(x) = 4*x^3-6*x^2 ƒ"(x) = 12*x^2-12*x Nollakohdat: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾ N1( 1 | 0 ) m = -2 N2( 1,83929 | 0 ) m = 4,5912 Ääriarvot: ‾‾‾‾‾‾‾‾‾‾‾‾ T1( 1,5 |-0,6875 ) m = 0 Taitepisteet: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ W1( 0 | 1 ) m = 0 W2( 1 | 0 ) m = -2
Newton-iterointi
Newton-iterointi on lähentymismenetelmä funktion ƒ(x) nollakohdan laskemiseksi. Kun annetaan aloitusarvo x0, joka on riittävän lähellä etsittyä nollakohtaa, seuraava likiarvo saadaan tangentin leikkauksena funktion ƒ kuvaajaan pisteessä
ƒ(x) = x-cos(x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
Integraalilaskenta
(helmikuusta 2021 kaaripituuksilla)
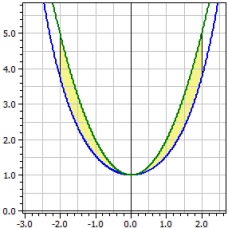
Lasketaan kahden funktiokäyrän välisen alueen suunnattu ja absoluuttinen ala annetussa välivälissä.
Lisäksi määritetään:
- momentit pyörityksessä x- ja y-akselin ympärillä,
- pyörityksessä syntyvät kappaleiden tilavuudet,
- kaaripituudet välivälissä [a;b] ja
- alueen painopiste (kun A1=A2).
ƒ1(x) = cosh(x) ƒ2(x) = x^2+1 Integraatioväli [a;b] -2 ... 2 Suunnattu ala : A1 = -2,07961 Absoluuttinen ala : A2 = 2,07961 Kaaripituudet : L1[a;b] = 7,254 L2[a,b] = 9,294
Sarjakehitelmä
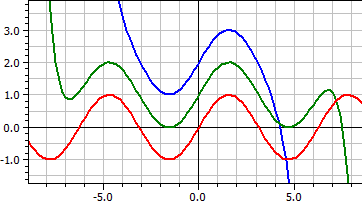
Piirretään sarjana annettu funktio, jossa sarjakehitelmät eri parametrialueilla voidaan vertailla ja erottaa toisistaan siirtämällä ne y-suunnassa.
Sinifunktion Taylor-sarjan ensimmäiset 16 termiä. ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) , k = 4, 8 ja 16
Pinta-alafunktiot
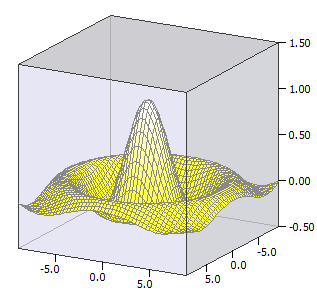
Piirretään pinta-alafunktio ƒ(x,y), eli kahden muuttujan funktion kolmiulotteinen kuvaaja.
Esimerkki:
ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)
-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5
