MatheAss 10.0 − 3-ulotteinen geometria
Koordinaatistot
Tällä ohjelmalla voidaan muuntaa kolmiulotteiset kartesiolaiset koordinaatit pallokoordinaateiksi tai sylinterikoordinaateiksi ja päinvastoin.
kartesiolainen polaarinen sylinterinen x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Platonin kappaleet
Ohjelma laskee viisi Platonin kappaletta: tetraedrin, heksaedrin, oktaedrin, dodekaedrin ja ikosaedrin, kun sivunpituus, pinnan korkeus, tilavuuskorkeus, sisäpallon säde, ympärpallon säde, tilavuus tai pinta-ala on annettu.
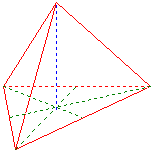
Tetraedri
Annettu:
¯¯¯¯¯¯¯¯
Ympärpallon säde ru = 1
Tulokset:
¯¯¯¯¯¯¯¯¯¯
Sivu a = 1,6329932
Pinnan korkeus h1 = 1,4142136
Tilavuuskorkeus h2 = 1,3333333
Sisäpallon säde ri = 0,33333333
Tilavuus V = 0,51320024
Pinta-ala O = 4,6188022
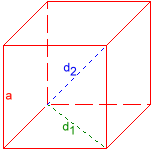
Heksaedri
Annettu:
¯¯¯¯¯¯¯¯
Pinta-ala O = 8
Tulokset:
¯¯¯¯¯¯¯¯¯¯
Sivu a = 1,1547005
Pinnan diagonaali d1 = 1,6329932
Tilavuusdiagonaali d2 = 2
Ympärpallon säde ru = 1
Sisäpallon säde ri = 0,57735027
Tilavuus V = 1,5396007
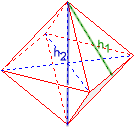
Oktaedri
Annettu:
¯¯¯¯¯¯¯¯
Tilavuus V = 4/3
Tulokset:
¯¯¯¯¯¯¯¯¯¯
Sivu a = 1,4142136
Pinnan korkeus h1 = 1,2247449
Tilavuuskorkeus h2 = 2
Ympärpallon säde ru = 1
Sisäpallon säde ri = 0,57735027
Pinta-ala O = 6,9282032
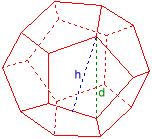
Dodekaedri
Annettu:
¯¯¯¯¯¯¯¯
Pinnan diagonaali d = 2
Tulokset:
¯¯¯¯¯¯¯¯¯
Sivu a = 1,236068
Pinnan korkeus h = 1,902113
Ympärpallon säde ru = 1,7320508
Sisäpallon säde ri = 1,3763819
Tilavuus V = 14,472136
Pinta-ala O = 31,543867
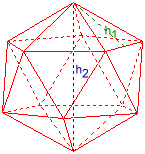
Ikosaedri
Annettu:
¯¯¯¯¯¯¯¯
Tilavuuskorkeus h2 = 2
Tulokset:
¯¯¯¯¯¯¯¯¯
Sivu a = 1,0514622
Pinnan korkeus h1 = 0,910593
Ympärpallon säde ru = 1
Sisäpallon säde ri = 0,79465447
Tilavuus V = 2,5361507
Pinta-ala O = 9,5745414
Muut kappaleet
Ohjelma laskee kaikki suureet säännölliselle prismalle, pystysuoralle ympyräsylinterille, neliöpyramidille, pystysuoralle ympyräkartiolle tai pallolle, kun kaksi niistä on annettu.
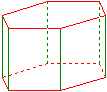
Prisma
Annettu: n = 4
¯¯¯¯¯¯¯¯
Tilavuus V = 1
Pinta-ala O = 6
Tulokset:
¯¯¯¯¯¯¯¯¯
Sivu a = 1
Korkeus h = 1
Ympäriympyrän säde ru = 0,70710678
Sisäympyrän säde ri = 0,5
Pohja-ala G = 1
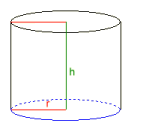
Ympyräsylinteri
Annettu:
¯¯¯¯¯¯¯¯
Säde r = 1
Tilavuus V = 1
Tulokset:
¯¯¯¯¯¯¯¯¯¯
Korkeus h = 0,31830989
Ympärysmitta u = 6,2831853
Pohja-ala G = 3,1415927
Mantelipinta M = 2
Pinta-ala O = 8,2831853
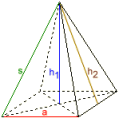
Neliöpyramidi
Annettu:
¯¯¯¯¯¯¯¯
Pohjan sivu a = 1
Tilavuus V = 1
Tulokset:
¯¯¯¯¯¯¯¯¯
Sivusärmä s = 3,082207
Tilavuuskorkeus h1 = 3
Sivukorkeus h2 = 3,0413813
Pinta-ala O = 7,0827625
Sivupinta A = 1,5206906
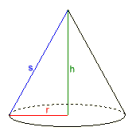
Ympyräkartio
Annettu:
¯¯¯¯¯¯¯¯
Tilavuus V = 1
Pohja-ala G = 1
Tulokset:
¯¯¯¯¯¯¯¯¯¯
Säde r = 0,56418958
Korkeus h = 3
Sivujana s = 3,0525907
Mantelipinta M = 5,4105761
Pinta-ala O = 6,4105761
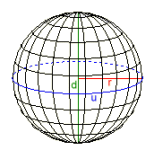
Pallo
Annettu:
¯¯¯¯¯¯¯¯
Pinta-ala O = 1
Tulokset:
¯¯¯¯¯¯¯¯¯¯
Säde r = 0,28209479
Halkaisija d = 0,56418958
Ympärysmitta u = 1,7724539
Tilavuus V = 0,094031597
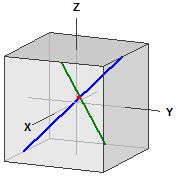
Suora kahden pisteen kautta
Suora A(1|1|1), B(2|5|6)
Parametriesitys
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
x = ⎪ 1 ⎪ + t·⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 5 ⎭
Etäisyys origosta
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 0,78679579
Sijainti xy-tasoon nähden
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Ortogonaaliproj.: 4·x - y = 3
Leikkauspiste: S1(0,8|0,2|0)
Leikkauskulma: 50,490288°
Sijainti yz-tasoon nähden
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Ortogonaaliproj.: 5·x - 4·y = 1
Leikkauspiste: S2(0|-3|-4)
Leikkauskulma: 8,8763951°
Sijainti xz-tasoon nähden
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Ortogonaaliproj.: 5·x - y = 4
Leikkauspiste: S3(0,75|0|-0,25)
Leikkauskulma: 38,112927°
Taso kolmen pisteen kautta
Taso pisteiden kautta:
A(1|2|3), B(2|3|3), C(1|0|1)
Piste-suunta-muoto:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
Koordinaattiyhtälö:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Etäisyys origosta:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Jälkipisteet:
¯¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)
Pallo neljän pisteen kautta
Pallo pisteiden kautta:
A(1|0|0), B(0|2|0),
C(0|0|3), D(1|0|1)
Normaalimuoto:
¯¯¯¯¯¯¯¯¯¯¯
| -> ⎧-2,5 ⎫ |2
K: | x - ⎪-0,5 ⎪ | = 12,75
| ⎩ 0,5 ⎭ |
Keskipiste ja säde:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-2,5|-0,5|0,5)
r = 3,5707142
Leikkaukset avaruudessa
Ohjelma laskee suorien, tasojen ja pallojen leikkaukset.
kaksi suoraa
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Leikkauspiste : S(5|5|5)
Leikkauskulma: 60°
Etäisyydet origosta :
d(O,g)=5 d(O,h)=5
Taso ja suora
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
E : x + y + z = 5
Leikkauspiste : S(5|0|0)
Leikkauskulma: 54,73561°
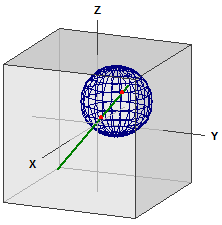
Pallo ja suora
-> ⎧ 1 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
K : M(5|5|5) , r = 5
Leikkauspisteet :
S1(2,8187|1,8187|1,8187)
S2(8,5147|7,5147|7,5147)
Jänteen pituus :
s = 9,8657657
kaksi tasoa
Annettu ovat tasot:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1 : 5·x - 2·y = 5
E2 : 2·x - y + 5·z = 8
Tasojen leikkaussuora:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> |-11 | | 10 |
g : x = |-30 | + r·| 25 |
| 0 | | 1 |
Etäisyys origosta:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,5057283
Tasojen leikkauskulma:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 65,993637°
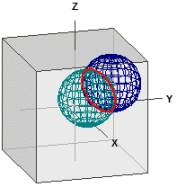
kaksi palloa
Annettu ovat pallot: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ K1 : M1(3|3|3) , r1 = 3 K2 : M2(1|1|1) , r2 = 3 Leikkausympyrä: ¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2), r = 2,4494897 Leikkaustaso: ¯¯¯¯¯¯¯¯¯¯¯¯¯ E : x + y + z = 6
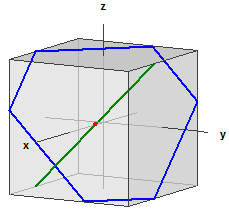
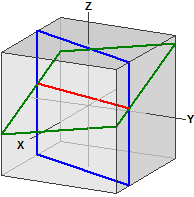
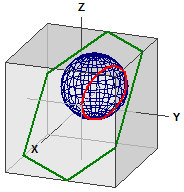
Pallo ja taso
Taso :
¯¯¯¯¯¯¯
E : 5·x - 4·y + 5·z = -3
Pallo :
¯¯¯¯¯¯¯
| -> ⎧ 1 ⎫|2
K : | x - ⎪ 2 ⎪| = 16
| ⎩ 3 ⎭|
Pallon ja tason leikkausympyrä :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-0,13636|2,9091|1,8636)
r = 3,548367
Etäisyydet pallolla
(Uutta versiossa 9.0 joulukuusta 2021)
Ohjelma laskee etäisyyden kahden pisteen välillä pallolla. Tässä yhdistetään useita MatheAssin toimintoja.
GPS desimaali ¯¯¯¯¯¯¯¯¯¯¯ Berliini : 52.523403, 13.4114 New York : 40.714268, -74.005974 GPS asteet-minuutit-sekunnit ¯¯¯¯¯¯¯ Berliini : 52° 31' 24.2508" N, 13° 24' 41.0400" E New York : 40° 42' 51.3648" N, 74° 0' 21.5064" W . . . Etäisyys ¯¯¯¯¯¯¯¯¯¯ d = r · α [rad] = 6385,112
