MatheAss 10.0 − Lineaarinen algebra

Lineaariset yhtälöjärjestelmät

Ohjelma määrittää ratkaisuvektorin lineaarisesta yhtälöjärjestelmästä, jossa on n yhtälöä ja n tuntematonta.

Esimerkki: Jos haetaan paraabeli pisteiden P(1/3), Q(2/1) ja R(4/9) kautta, saadaan yhtälöjärjestelmä

  1·x1 + 1·x2 + 1·x3 = 3
  4·x1 + 2·x2 + 1·x3 = 1
 16·x1 + 4·x2 + 1·x3 = 9   
            
 L = ( 2; -8; 9 )

Paraabelin yhtälö on siis y = 2x² - 8x + 9.

Esimerkki, jossa ratkaisutila on kaksiulotteinen:

  0·x1 + 0·x2 + 2·x3 - 1·x4  =  1
  1·x1 + 1·x2 + 1·x3 + 1·x4  =  4
  2·x1 + 2·x2 - 4·x3 + 5·x4  =  5
  1·x1 + 1·x2 - 7·x3 + 5·x4  =  0

  L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }

Lineaarinen optimointi (helmikuusta 2022)

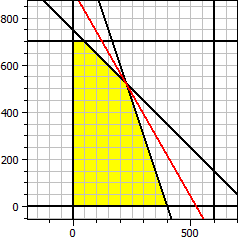
Ohjelma määrittää optimaalisen ratkaisun tavoitefunktiolle, jossa on kaksi muuttujaa ja lineaariset epäyhtälörajoitukset.

Tavoitefunktio:   
  ƒ(x,y) = 140·x + 80·y → Maksimi

Rajoitukset:
  x ≥ 0
  y ≥ 0
  x ≤ 600
  y ≤ 700
  x + y ≤ 750
  3·x + y ≤ 1200

Maksimi
  x = 225   y = 525
  ƒ(x,y) = 73500

Lineaarikombinaatio

Ohjelma määrittää vektorin lineaarikombinaation kolmesta annetusta vektorista. Rutiinia voidaan käyttää myös kolmen vektorin lineaarisen riippumattomuuden tarkistamiseen avaruudessa, eli siihen, sijaitsevatko ne samassa tasossa.

    ⎧ 1 ⎫     ⎧ 2 ⎫     ⎧ 0 ⎫   ⎧ 2 ⎫
  a·⎪ 2 ⎪ + b·⎪ 1 ⎪ + c·⎪ 1 ⎪ = ⎪ 3 ⎪   
    ⎩ 0 ⎭     ⎩ 1 ⎭     ⎩ 0 ⎭   ⎩ 7 ⎭

Ratkaisu :
  a = -12  b = 7  c = 20

Skalaaritulo

Ohjelma laskee kahden vektorin skalaaritulon, kummankin vektorin pituuden ja niiden välisen kulman.

   ->  ⎧ 1 ⎫   ->  ⎧ 5 ⎫
   a = ⎪ 3 ⎪   b = ⎪ 0 ⎪
       ⎩ 1 ⎭       ⎩ 3 ⎭

Vektorien skalaaritulo = 8

Ensimmäisen vektorin pituus = √11 = 3,3166248
Toisen vektorin pituus      = √34 = 5,8309519

Välinen kulma  α = 65,564402°

Vektoritulo

Ohjelma laskee kahden vektorin vektoritulon sekä sen itseisarvon. Vektoritulo on kohtisuora niiden jännittämään rinnakkaisnelikulmioon, ja sen itseisarvo on yhtä suuri kuin rinnakkaisnelikulmion pinta-ala.

     ->  ⎧ 1 ⎫     ->  ⎧ 7 ⎫
     a = ⎪ 2 ⎪     b = ⎪ 1 ⎪
         ⎩ 3 ⎭         ⎩ 4 ⎭

 ->  ->  ⎧  5 ⎫    ->  ->  
 a x b = ⎪ 17 ⎪   |a x b|= √483 = 21,977261
         ⎩-13 ⎭

Tilavuustulo

Ohjelma laskee kolmen vektorin tilavuustulon. Sen itseisarvo antaa niiden jännittämän siirretyn suorakulmaisen särmiön (spatin) tilavuuden.

  ->  ⎧ 2 ⎫     ->  ⎧ 2 ⎫     ->  ⎧ 3 ⎫   
  a = ⎪ 3 ⎪     b = ⎪-1 ⎪     c = ⎪ 9 ⎪
      ⎩ 5 ⎭         ⎩ 7 ⎭         ⎩ 2 ⎭

    ->  ->    ->  
  ( a x b ) · c = 26

Matriisin käänteinen

Ohjelma laskee n-asteiselle neliömatriisille determinantin, asteen ja käänteismatriisin.

Matriisi: 

  ⎧  0  1  1  ⎫
  ⎪  0  1  3  ⎪
  ⎩  2  0  1  ⎭

Käänteismatriisi

  ⎧  0,25 -0,25  0,5  ⎫
  ⎪   1,5  -0,5    0  ⎪
  ⎩  -0,5   0,5    0  ⎭

Aste = 3,  Aste (Rang) = 3,  Determinantti = 4

Pseudoinversi

Jos matriisin A sarakkeet ovat lineaarisesti riippumattomia, niin A^T· A on käänteinen ja saadaan seuraavalla kaavalla pseudoinversi:

A⁺ = ( A^T· A )^-1· A^T

Tällöin A⁺ on vasen käänteinen matriisille A , eli pätee: A⁺ · A = E .

Matriisi A
¯¯¯¯¯¯¯¯
  ⎧  1  1  1  1  ⎫
  ⎩  5  7  7  9  ⎭

A^T· A
¯¯¯¯
  ⎧  26  36  36  46  ⎫
  ⎪  36  50  50  64  ⎪
  ⎪  36  50  50  64  ⎪
  ⎩  46  64  64  82  ⎭

A^T· A ei käänteinen

A · A^T
¯¯¯¯¯¯
  ⎧   4   28  ⎫
  ⎩  28  204  ⎭

( A · A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯
  ⎧  6,375 -0,875  ⎫
  ⎩ -0,875  0,125  ⎭

Oikea käänteinen:  A^T · ( A · A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧     2  -0,25  ⎫
  ⎪  0,25      0  ⎪
  ⎪  0,25      0  ⎪
  ⎩  -1,5   0,25  ⎭

Matriisikertolasku

Ohjelma laskee kahden matriisin tulomatriisin.

 1. Matriisi           2. Matriisi

  ⎧  1  2  3  0  ⎫   ⎧  1   2   3   4  ⎫
  ⎪  4  5  6  0  ⎪   ⎪  5   6   7   8  ⎪
  ⎪  0  0  0  0  ⎪   ⎪  9  10  11  12  ⎪
  ⎩  0  0  0  0  ⎭   ⎩  0   0   0   0  ⎭

 Tulomatriisi
  
  ⎧  38  44   50   56  ⎫
  ⎪  83  98  113  128  ⎪
  ⎪   0   0   0    0   ⎪
  ⎩   0   0   0    0   ⎭

MatheAss 10.0 − Lineaarinen algebra

A+ = ( AT· A )-1· AT

A⁺ = ( A^T· A )^-1· A^T