MatheAss 10.0 − Stokastiikka

Tilastot

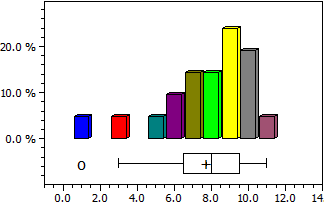
Annetusta datalistasta määritetään keskiarvo (aritmeettinen keskiarvo), mediaani, varianssi ja keskihajonta. Lisäksi jakauma esitetään histogrammina ja laatikkokaaviona (box-plot).

Data:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8

Datamäärä           n = 21
Maksimi            max = 11
Minimi               min = 1
Keskiarvo             x = 7,7142857
Mediaani               c = 8
Varianssi              s² = 6,1142857
Keskihajonta        s = 2,4727082

Regressio

Tällä rutiinilla voidaan suorittaa mittaussarjalle käyränsovitus. Voit valita seuraavista sovituksista ja tarvittaessa siirtää tai venyttää kaikkia pisteitä x- tai y-suunnassa.

Origo-suora ( y = a·x )

Lineaarinen regressio ( y = a·x + b )

Polynomiregressio n-aste ( y = a₀ + ... + a_n·xⁿ )

Geometrinen regressio ( y = a·x^b )

Eksponentiaalinen regressio ( y = a·b^x )

Logaritminen regressio ( y = a + b·ln(x) )

Yhdessä kuvaajan kanssa tulostetaan sovituskäyrän funktiolauseke, selitysaste (R²), korrelaatiokerroin ja keskihajonta.

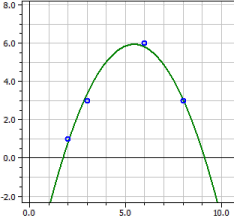
Polynomiregressio

y =  − 2,6299435
      + 3,8516949·x
      − 0,43361582·x²

Selitysaste             = 0,98338318
Korrelaatiokerroin  = 0,99165679        
Keskihajonta         = 0,46028731

Logistinen regressio (Uutta versiossa 9.0)

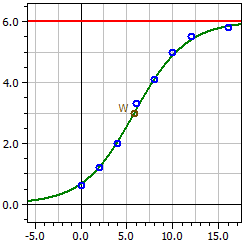
Ohjelma määrittää mittaussarjalle logistisen funktion sovituksen
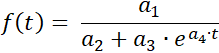
parametreilla a₁ = ƒ(0)·S , a₂ = ƒ(0) , a₃ = S - ƒ(0) , ja a₄ = -k·S sekä kyllästysraja S .

Data: "Hopfenwachstum.csv"

Kyllästysraja: 6
         Piiloluku: 1

                                 4,0189
ƒ(x) = ————————————————
             0,66981 + 5,3302 · e^(-0,35622·t)

Taitepiste W(5,8226/3)

Maksimi kasvunopeus  ƒ'(xw) = 0,53433

8 arvoa 
Selitysaste             = 0,99383916
Korrelaatiokerroin      = 0,99691482
Keskihajonta            = 0,16172584

Kombinatoriikka

Lasketaan mahdollisuuksien määrä, kun n alkioista valitaan k, jos järjestyksellä on merkitystä tai ei, ja jos toistoja sallitaan tai ei.

n = 49 ,  k = 6

Järjestetty valinta ilman toistoa = 10 068 347 520
Järjestetty valinta toiston kanssa = 13 841 287 201
Järjestämätön valinta ilman toistoa = 13 983 816
Järjestämätön valinta toiston kanssa = 25 827 165

Permutaatiot k :                k ! = 720

Binomijakauma

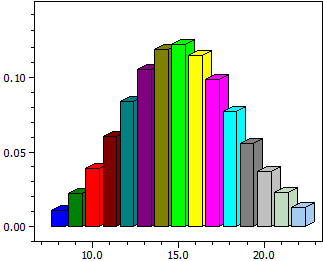
Lasketaan b(k;n;p)-jakaumaa noudattavalle satunnaismuuttujalle X annetulla n ja p.

- pylväskuva todennäköisyyksistä P( X = k )
- niiden numeeriset arvot välivälissä [k-min;k-max]
- todennäköisyys P( k-min <= X <= k-max)

n = 50             p = 0,3

    k             P(X=k)         P(0<=X<=k) 
  ¯¯¯¯    ¯¯¯¯¯¯¯¯¯¯     ¯¯¯¯¯¯¯¯¯¯
    8         0,01098914     0,01825335
    9         0,02197829     0,04023163
  10        0,03861899     0,07885062
  11        0,06018544     0,13903606
  12        0,08382972     0,22286578
  13        0,10501745     0,32788324
  14        0,11894834     0,44683157
  15        0,12234686     0,56917844
  16        0,11470018     0,68387862
  17        0,09831444     0,78219306
  18        0,07724706     0,85944012
  19        0,05575728     0,91519740
  20        0,03703876     0,95223616
  21        0,02267679     0,97491296
  22        0,01281092     0,98772387
  ¯¯¯¯    ¯¯¯¯¯¯¯¯¯¯     ¯¯¯¯¯¯¯¯¯¯
  P(8<=k<=22) =            0,98045967

Hypergeometrinen jakauma

Lasketaan h(k;n;m;r)-jakaumaa noudattavalle satunnaismuuttujalle X annetulla n, m ja r. Tuloksena saadaan pylväskuva ja taulukko todennäköisyyksistä P(X=k).

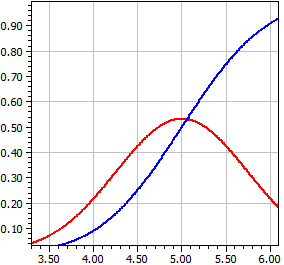
Normaalijakauma

Lasketaan N(µ,σ²)-jakaumaa noudattavalle satunnaismuuttujalle X annetulla odotusarvolla µ ja varianssilla σ² tiheysfunktio ƒ(x) ja kertymäfunktio Φ(x), eli integraali yli ƒ(x).

  μ = 5              σ = .75

      x                      ƒ(x)                Φ(x)   
  ¯¯¯¯¯¯¯¯¯¯  ¯¯¯¯¯¯¯¯¯¯  ¯¯¯¯¯¯¯¯¯¯
  2                    0,00017844   0,00003167
  2,33333333   0,00095649   0,00018859
  2,66666666   0,00420802   0,00093192
  2,99999999   0,01519465   0,00383038
  3,33333332   0,04503153   0,01313415
  3,66666665   0,10953585   0,03772017
  3,99999998   0,21868009   0,09121120
  4,33333331   0,35832381   0,18703139
  4,66666664   0,48189843   0,32836063
  4,99999997   0,53192304   0,49999998
  5,3333333     0,48189845   0,67163934
  5,66666663   0,35832383   0,81296859
  5,99999996   0,21868012   0,90878878
  6,33333329   0,10953586   0,96227982
  6,66666662   0,04503154   0,98686585
  6,99999995   0,01519465   0,99616962
  7,33333328   0,00420802   0,99906808
  7,66666661   0,00095649   0,99981141
  7,99999994   0,00017844   0,99996833