MatheAss 10.0 − Алгебра

Простi числа

Програма обчислює всi простi числа мiж двома числами.

Простi числа мiж 1000000000 та 1000000300:

1000000007 1000000009 1000000021 1000000033 1000000087 1000000093
1000000097 1000000103 1000000123 1000000181 1000000207 1000000223
1000000241 1000000271 1000000289 1000000297

16 простих чисел

Простi числовi пари (Нове у версiї 9.0)

Програма визначає в iнтервалi [a,b] усi простi двiйки (p,p+2), простi "кузени" (p,p+4), "сексуальнi простi" (p,p+6) та простi трiйки.

Простi трiйки мiж 1 та 200

(3|5|7) (5|7|11) [7|11|13] (11|13|17) [13|17|19] (17|19|23) [37|41|43] 
(41|43|47) [67|71|73] [97|101|103] (101|103|107) [103|107|109] (107|109|113)
(191|193|197) [193|197|199] 

15 простих трiйок
7 форми (p|p+2|p+6) та 7 форми [p|p+4|p+6]

Розклад на простi множники

Програма розкладає натуральнi числа на їх простi степенi.

  99999999999901 = 19001 · 5262880901
  99999999999001 = 107 · 401 · 1327 · 1756309
  99999999990001 = просте число 
    3938980639167 = 3¹⁴ · 7⁷
999330136292431 = 99971² · 99991

НСД та НСК

Для двох чисел a та b визначаються найбiльший спiльний дiльник, найменше спiльне кратне та їх множини дiльникiв.

a = 24
b = 256

найбiльший спiльний дiльник               НСД = 8
найменше спiльне кратне                   НСК = 768  

Множини дiльникiв :
T(a) = { 1 2 3 4 6 8 12 24}
T(b) = { 1 2 4 8 16 32 64 128 256}

Вiдсотковi обчислення (Нове у версiї 9.0)

Обчислюються базове значення G, вiдсоткове значення W, вiдсоткова ставка p або p%, коефiцiєнт росту q та кiнцеве значення E, якщо задано два незалежнi параметри.

Дано:
¯¯¯¯¯¯¯¯
        Вiдсоткове значення  W = −120
Коефiцiєнт росту  q = 95% = 0,95 = 19/20

Результати:
¯¯¯¯¯¯¯¯¯¯
          Базове значення  G = 2400
     Вiдсоткова ставка  p% = −5% = −0,05 = −1/20      
              Кiнцеве значення  E = 2280

Десятковi числа у дроби

Програма перетворює перiодичнi та скiнченнi десятковi дроби у звичайнi дроби.

Неперiодична частина : 1.20
Перiод : 045
    ___
1.20045 = 120/100 + 1/2220 = 533/444

Дроби у десятковi числа

Програма перетворює дроби у перiодичнi десятковi дроби та визначає перiод i його довжину.

Чисельник : 533
Знаменник : 444
              ___
533/444 = 1.20045
перiодичнiсть починається з 3-ї цифри пiсля коми
перiод має довжину 3 цифри

Бiномi

До найвiдомiших формул шкiльної математики належить бiномiчна формула (a + b)² = a² + 2ab + b² .

Програма обчислює загальнiший випадок (a·x + b·y)ⁿ.

(2·x  − 3·y)⁷ =       +128 · x⁷
                           −1344 · x⁶ · y
                            +6048 · x⁵ · y²
                          −15120 · x⁴ · y³   
                          +22680 · x³ · y⁴
                          −20412 · x² · y⁵
                          +10206 · x · y⁶
                            −2187 · y⁷

Програма знаходить дiйснi розв'язки рiвняння 4-го або нижчого степеня. Для рiвнянь вищого степеня, окрiм наближених обчислень (нульовi точки у модулi дослiдження кривих), не iснує алгебраїчного методу розв'язання.

x⁴ + 2·x³ - 3·x² + 5·x - 5 = 0   <=>   (x - 1)·(x³ + 3·x² + 5) = 0
L = {-3,42599;  1}

Дiофантовi рiвняння

Названi на честь Дiофанта з Александрiї (близько 250 р.), який у своїй книзi Arithmetica розглядав розв'язання лiнiйних та квадратних рiвнянь, зокрема їх цiлочисельнi розв'язки.
Програма обчислює цiлочисельнi розв'язки рiвняння a·x - b·y - c = 0. Таким чином можна визначити цiлочисельнi точки на прямiй.

7·x − 3·y − 5 = 0 ;   x,y цiлi числа
L = { ( 2 + 3t | 3 + 7t ) }

Пiфагоровi числовi трiйки

Пiфагоровi числовi трiйки — це цiлочисельнi розв'язки (x,y,z) рiвняння x² + y² = z² , яке виконується для сторiн прямокутних трикутникiв.

Для x, y, z мiж 100 та 400 отримуємо:

( 119, 120, 169 )    ( 104, 153, 185 )    ( 133, 156, 205 )    ( 105, 208, 233 )    
( 140, 171, 221 )    ( 115, 252, 277 )    ( 120, 209, 241 )    ( 161, 240, 289 )    
( 160, 231, 281 )    ( 207, 224, 305 )    ( 175, 288, 337 )    ( 135, 352, 377 )    
( 136, 273, 305 )    ( 204, 253, 325 )    ( 225, 272, 353 )    ( 189, 340, 389 )    
( 180, 299, 349 )    ( 252, 275, 373 )    ( 152, 345, 377 )    ( 228, 325, 397 )

Калькулятори

Є чотири калькулятори:

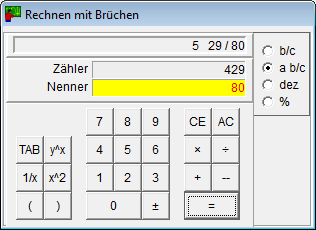
Калькулятор для дробiв виконує чотири арифметичнi дiї та може пiдвищувати до степеня.
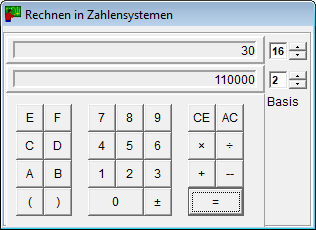
Калькулятор для систем числення працює з будь-якою основою вiд 2 до 16.
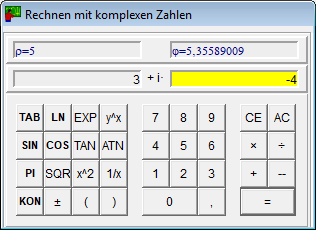
Калькулятор для комплексних чисел обчислює крiм звичних функцiй також спряжене комплексне число.
Калькулятор для великих цiлих чисел виконує арифметичнi дiї та формули комбiнаторики.

Обчислення з великими числами (Нове у версiї 9.0 з квiтня 2021)

Обчислення проводяться з цiлими числами до максимуму 10 000 цифр.

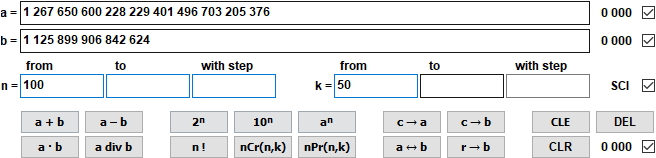
1 267 650 600 228 229 401 496 703 205 376   div  1 125 899 906 842 624  
 =  1 125 899 906 842 624  залишок  0
 =  1,13 · 10^15 залишок 0

nCr(100,50)  =  100 891 344 545 564 193 334 812 497 256 = 1,01 · 10^29