MatheAss 10.0 − Стохастика
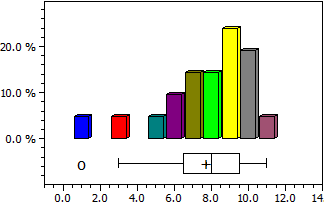
Статистика
Для списку даних визначаються середнє значення (арифметичне середнє), медіана, дисперсія та стандартне відхилення. Додатково будується розподіл у вигляді гістограми та Box-Plot.
Дані:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8
Кількість даних n = 21
Максимум max = 11
Мінімум min = 1
Середнє значення x = 7,7142857
Медіана c = 8
Дисперсія s² = 6,1142857
Стандартне відхилення s = 2,4727082
 Регресія
Регресія
За допомогою цієї процедури можна виконати апроксимацію кривої для ряду вимірів. Можна обрати між такими видами апроксимації та за потреби всі точки змістити або розтягнути у напрямку x чи y.
Пряма через початок координат ( y = a·x )
Лінійна регресія ( y = a·x + b )
Поліноміальна регресія n-го порядку ( y = a0 + ... + an·xn )
Геометрична регресія ( y = a·xb )
Експоненціальна регресія ( y = a·bx )
Логарифмічна регресія ( y = a + b·ln(x) )
Разом із графіком виводяться функціональний вираз наближеної кривої, коефіцієнт детермінації, коефіцієнт кореляції та стандартне відхилення.
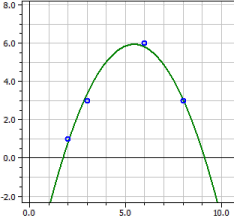
Поліноміальна регресія
y = − 2,6299435
+ 3,8516949·x
− 0,43361582·x2
Коефіцієнт детермінації = 0,98338318
Коефіцієнт кореляції = 0,99165679
Стандартне відхилення = 0,46028731
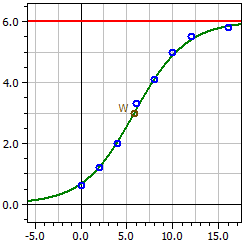
 Логістична регресія (Нове у версії 9.0)
Логістична регресія (Нове у версії 9.0)
Програма визначає для ряду вимірів апроксимацію кривої логістичною функцією
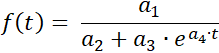
з параметрами
a1 = ƒ(0)·S , a2 = ƒ(0) , a3 = S - ƒ(0) ,
та a4 = -k·S і межею насичення S .
Дані з: "Hopfenwachstum.csv"
Межа насичення: 6
Приховане значення: 1
4,0189
ƒ(x) = ————————————————
0,66981 + 5,3302 · e^(-0,35622·t)
Точка перегину W(5,8226/3)
Максимальна швидкість росту ƒ'(xw) = 0,53433
8 значень
Коефіцієнт детермінації = 0,99383916
Коефіцієнт кореляції = 0,99691482
Стандартне відхилення = 0,16172584
 Комбінаторика
Комбінаторика
Обчислюються кількості можливостей вибрати з n елементів k, якщо враховується порядок або ні та якщо повторення допускаються або ні.
n = 49 , k = 6 Впорядкований вибір без повторень = 10 068 347 520 Впорядкований вибір з повторенням = 13 841 287 201 Невпорядкований вибір без повторень = 13 983 816 Невпорядкований вибір з повторенням = 25 827 165 Пермутації з k : k ! = 720
 Біноміальний розподіл
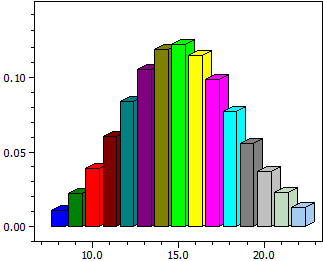
Біноміальний розподіл
Обчислюється для випадкової величини X, що має розподіл b(k;n;p) при фіксованих n та p:
- стовпчаста діаграма ймовірностей P( X = k )
- їх числові значення в інтервалі [k-min;k-max]
- ймовірність P( k-min <= X <= k-max)
n = 50 p = 0,3
k P(X=k) P(0<=X<=k)
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
8 0,01098914 0,01825335
9 0,02197829 0,04023163
10 0,03861899 0,07885062
11 0,06018544 0,13903606
12 0,08382972 0,22286578
13 0,10501745 0,32788324
14 0,11894834 0,44683157
15 0,12234686 0,56917844
16 0,11470018 0,68387862
17 0,09831444 0,78219306
18 0,07724706 0,85944012
19 0,05575728 0,91519740
20 0,03703876 0,95223616
21 0,02267679 0,97491296
22 0,01281092 0,98772387
¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
P(8<=k<=22) = 0,98045967
 Гіпергеометричний розподіл
Гіпергеометричний розподіл
Обчислюється для випадкової величини X, що має розподіл h(k;n;m;r) при фіксованих n, m та r: будується стовпчаста діаграма та таблиця значень ймовірностей P( X = k ).
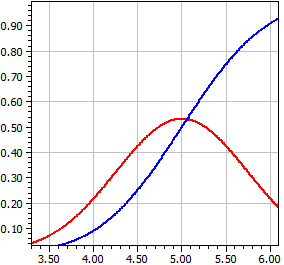
 Нормальний розподіл
Нормальний розподіл
Обчислюється для випадкової величини X, що має розподіл N(µ,σ²) з заданим математичним сподіванням µ та дисперсією σ²: визначаються функція густини ƒ(x) та функція розподілу Φ(x), тобто інтеграл від ƒ(x) .
μ = 5 σ = .75
x ƒ(x) Φ(x)
¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯
2 0,00017844 0,00003167
2,33333333 0,00095649 0,00018859
2,66666666 0,00420802 0,00093192
2,99999999 0,01519465 0,00383038
3,33333332 0,04503153 0,01313415
3,66666665 0,10953585 0,03772017
3,99999998 0,21868009 0,09121120
4,33333331 0,35832381 0,18703139
4,66666664 0,48189843 0,32836063
4,99999997 0,53192304 0,49999998
5,3333333 0,48189845 0,67163934
5,66666663 0,35832383 0,81296859
5,99999996 0,21868012 0,90878878
6,33333329 0,10953586 0,96227982
6,66666662 0,04503154 0,98686585
6,99999995 0,01519465 0,99616962
7,33333328 0,00420802 0,99906808
7,66666661 0,00095649 0,99981141
7,99999994 0,00017844 0,99996833