MatheAss 10.0 − 2-вимiрна Геометрiя

Прямокутнi трикутники

Якщо заданi двi з наведених величин, програма обчислює iншi. 

Дано:
¯¯¯¯¯¯¯¯
 Вiдрiзок гiпотенузи  p = 1,8
    Площа  A = 6 
 
Результати:
¯¯¯¯¯¯¯¯¯¯
              Катет  a = 3
              Катет  b = 4
       Гiпотенуза  c = 5
               Кут  α = 36,869898°
               Кут  β = 53,130102°  
 Вiдрiзок гiпотенузи  q = 3,2
                 Висота  h = 2,4

Трикутники з трьох величин

З трьох зовнiшнiх величин (сторони або кути) трикутника програма обчислює сторони, кути, висоти, бiсектриси сторiн i кутiв, периметр та площу, а також центри i радiуси вписаного та описаного кiл. 

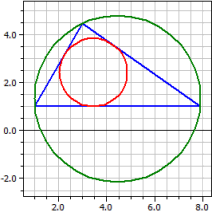
Дано: a=6, b=4 та α=60°

      Вершини:   A(1|1)         B(7,899|1)   C(3|4,4641)
      Сторони:   6                4                  6,89898
     Кути:   60°             35,2644°     84,7356° 
     Висоти:   3,98313      5,97469      3,4641 
  Бiсектриси сторiн:   4,77472      6,148          3,75513
  Бiсектриси кутiв:   4,38551      6,11664      3,5464

 Описане коло:   M(4,44949|1,31784)       ru = 3,4641
   Вписане коло:   O(3,44949|2,41421)        ri = 1,41421

    Площа: A = 11,9494      Периметр : u = 16,899
Трикутник 2

Трикутники з трьох точок

З координат трьох вершин програма обчислює всi зовнiшнi та внутрiшнi величини (див. Трикутники з трьох величин). 

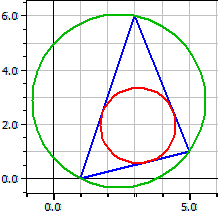
      Вершини : A(1|0)          B(5|1)          C(3|6) 
     Сторони : 5,38516       6,32456       4,12311
     Кути : 57,5288°     82,2348°     40,2364° 
     Висоти : 4,0853        3,47851       5,33578
  Бiсектриси сторiн : 4,60977       3,60555       5,5 
 Бiсектриси кутiв : 4,37592       3,51849       5,46225

 Описане коло : M(2,40909|2,86364)     ru = 3,19154
   Вписане коло :  O(3,11866|1,96195)      ri = 1,38952  
   
   Площа :  A = 11            Периметр : u = 15,8328
Трикутник 3

Особливi прямi та кола у трикутнику   (Нове у версiї 9.0)

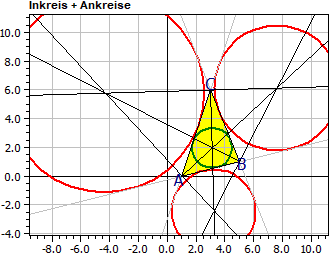
Програма визначає рiвняння серединних перпендикулярiв, бiсектрис сторiн, бiсектрис кутiв та висот трикутника. Крiм того, центри та радiуси описаного кола, вписаного кола, трьох зовнiшнiх кiл та кола Фейєрбаха (з березня 2025).

Дано:
¯¯¯¯¯¯¯¯
       Вершини:    A(1|0)   B(5|1)   C(3|6)
 
Результати:
¯¯¯¯¯¯¯¯¯¯
      Прямi:   a :  5·x + 2·y = 27
                    b :  3·x - y = 3
                    c :  x - 4·y = 1
 
     Вписане коло:    Mi(3,119|1,962)         r i = 1,390
 
  Зовнiшнi кола:    Ma(7,626|6,136)       ra = 4,346
                     Mb(-4,356|5,784)      rb = 6,910
                     Mc(3,248|-2,427)      rc = 2,900

Правильнi багатокутники

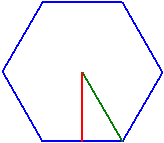
Якщо задано кiлькiсть вершин та одну з наведених величин, програма обчислює iншi.
Сторона a, радiус вписаного кола ri, радiус описаного кола ru, периметр u або площа A.

Дано:
¯¯¯¯¯¯¯¯
      Кiлькiсть вершин  n = 6
          Периметр  u = 8     
 
Результати:
¯¯¯¯¯¯¯¯¯¯
              Сторона  a = 1,3333333
Радiус описаного кола ru = 1,3333333
   Радiус вписаного кола ri = 1,1547005
            Площа  A = 4,6188022                        

Довiльнi багатокутники   (з листопада 2022)

Тепер також обчислюються сторони та кути багатокутника i перевiряється, чи є багатокутник опуклим, вгнутим або самопересiкаючим.
Крiм того, для опуклих багатокутникiв перевiряється, чи мають вони вписане i/або описане коло.

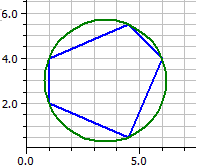
Вершини:                           Площа  A = 16
 A(1|2)                          
 B(4,5|0,5)                     Периметр  u = 15,54498
 C(6|4)                           
 D(4,5|5,5)                     Центр вершин: 
 E(1|4)                           ES(3,4|3,2)

                                     Центр площi: 
                                     FS(3,46875|3,07813)

Сторони:                          Кути:
 |AB| = 3,8078866          ∡BAE = 113,19859°
 |BC| = 3,8078866          ∡CBA = 90°
 |CD| = 2,1213203          ∡DCB = 111,80141°
 |DE| = 3,8078866          ∡EDC = 111,80141°
 |EA| = 2                         ∡AED = 113,19859°

Сeненний багатокутник
Описане коло:  M(3,5|3)  r=2,6925824

Сeненний багатокутник:

Вiдображення   (оновлено у версiї 9.0)

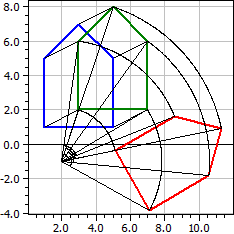
Програма дозволяє застосувати до n-кутника послiдовнiсть вiдображень. Можна вибрати зсув, дзеркальне вiдображення в прямiй, дзеркальне вiдображення в точцi, обертання, центричне розтягнення та зсув. 

Початкове зображення
A(1|1), B(5|1), C(5|5), D(3|7), E(1|5)

Паралельний зсув: dx=2, dy=1  ☑
A1(3|2), B1(7|2), C1(7|6), D1(5|8), E1(3|6)

Обертання: Z(2|-1), α=-60°  ☑
A2(5,0981|-0,36603), B2(7,0981|-3,8301),    
C2(10,562|-1,8301), D2(11,294|0,90192), 
E2(8,5622|1,634)

Коло та частини кола

Якщо задано двi з наведених величин, програма обчислює iншi. 

Дано:
¯¯¯¯¯¯¯¯      
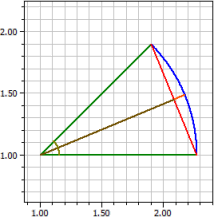
                 Дуга b = 1
                Кут α = 45°

Результати :
¯¯¯¯¯¯¯¯¯¯
                Радiус r = 1,2732395
                Хорда s = 0,97449536
      Сектор кола A1 = 0,63661977
             Вiдстань d = 1,17632
           Стрiла h = 0,096919589                
 Сегмент кола A2 = 0,063460604

        Площа кола A = 5,0929582
      Довжина кола u = 8

Дотичнi до кола   (Нове у версiї 9.0 з лютого 2021)

Обчислюються рiвняння таких дотичних:

  • Дотична до кола k у точцi B
  • Дотичнi до кола k через точку P поза колом
  • Дотичнi до кола k, паралельнi до прямої g
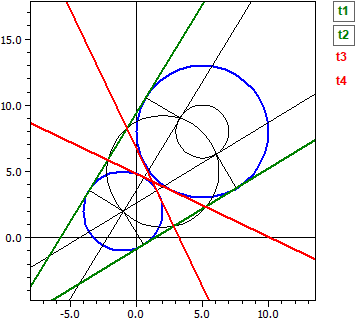
  • Дотичнi до двох кiл k1 та k2
Дано:
¯¯¯¯¯¯¯¯
  k1 : M(5|8) ,   r =5
  k2 : M(-1|2) ,   r =3

Зовнiшнi дотичнi
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t1: -4,2923·x + 7,04104·y = -6,36427
  t2: -7,04104·x + 4,29230·y = 40,3643

Внутрiшнi дотичнi
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t3: 1,21895·x + 2,55228·y = 12,3709
  t4: -2,55228·x − 1,21895·y = -8,3709

Площиннi перетини

Програма обчислює перетини прямих i кiл

двi прямi

g : x + y = 0
h : x - y = 5

Точка перетину : S(2,5|-2,5)

Кут перетину: 90°

Вiдстанi до початку координат :
  d(g,O) = 0
  d(h,O) = 3,5355339

Пряма i коло

k : M(5|0)   r = 5
g : x + y = 0

Точки перетину :
  S1(5|-5)    S2(0|0)     

двi кола

k1 : M1(5|5)   r1 = 5
k2 : M2(0|0)   r2 = 5

Точки перетину :
  S1(5|0)   S2(0|5)

Пряма, що з'єднує :   
  x + y = 5