MatheAss 10.0 − Лiнiйна алгебра

Системи лiнiйних рiвнянь

Програма визначає вектор розв’язку системи лiнiйних рiвнянь з n рiвняннями та n невiдомими.

Приклад: Якщо шукаємо параболу через точки P(1/3), Q(2/1) та R(4/9), це приводить до системи рiвнянь

  1·x1 + 1·x2 + 1·x3 = 3
  4·x1 + 2·x2 + 1·x3 = 1
 16·x1 + 4·x2 + 1·x3 = 9   
            
 L = ( 2; -8; 9 )

Отже, парабола має рiвняння y = 2x² - 8x + 9.

Приклад з двовимiрним простором розв’язкiв:

  0·x1 + 0·x2 + 2·x3 - 1·x4  =  1
  1·x1 + 1·x2 + 1·x3 + 1·x4  =  4
  2·x1 + 2·x2 - 4·x3 + 5·x4  =  5
  1·x1 + 1·x2 - 7·x3 + 5·x4  =  0

  L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }

Лiнiйна оптимiзацiя (з лютого 2022)

Програма визначає оптимальне рiшення для цiльової функцiї з двома змiнними та лiнiйними нерiвностями як обмеженнями.

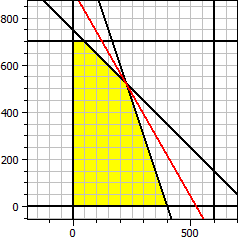
Цiльова функцiя:   
  ƒ(x,y) = 140·x + 80·y → максимум

Обмеження:
  x ≥ 0
  y ≥ 0
  x ≤ 600
  y ≤ 700
  x + y ≤ 750
  3·x + y ≤ 1200

Максимум
  x = 225   y = 525
  ƒ(x,y) = 73500

Лiнiйна комбiнацiя

Програма визначає лiнiйну комбiнацiю вектора з трьох заданих векторiв. Ця процедура також придатна для перевiрки лiнiйної незалежностi трьох векторiв у просторi, тобто чи лежать вони в однiй площинi.

    ⎧ 1 ⎫     ⎧ 2 ⎫     ⎧ 0 ⎫   ⎧ 2 ⎫
  a·⎪ 2 ⎪ + b·⎪ 1 ⎪ + c·⎪ 1 ⎪ = ⎪ 3 ⎪   
    ⎩ 0 ⎭     ⎩ 1 ⎭     ⎩ 0 ⎭   ⎩ 7 ⎭

Розв’язок :
  a = -12  b = 7  c = 20

Скалярний добуток

Програма обчислює для двох векторiв їх скалярний добуток, довжину обох векторiв та кут мiж ними.

   ->  ⎧ 1 ⎫   ->  ⎧ 5 ⎫
   a = ⎪ 3 ⎪   b = ⎪ 0 ⎪
       ⎩ 1 ⎭       ⎩ 3 ⎭

Скалярний добуток векторiв = 8

Довжина першого вектора   = √11 = 3,3166248
Довжина другого вектора   = √34 = 5,8309519

Кут мiж векторами  α = 65,564402°

Векторний добуток

Програма обчислює для двох векторiв їх векторний добуток та його модуль. Векторний добуток перпендикулярний до паралелограма, який вони утворюють, а його модуль дорiвнює площi цього паралелограма.

     ->  ⎧ 1 ⎫     ->  ⎧ 7 ⎫
     a = ⎪ 2 ⎪     b = ⎪ 1 ⎪
         ⎩ 3 ⎭         ⎩ 4 ⎭

 ->  ->  ⎧  5 ⎫    ->  ->  
 a x b = ⎪ 17 ⎪   |a x b|= √483 = 21,977261
         ⎩-13 ⎭

Мiшковий добуток

Програма обчислює для трьох векторiв їх мiшковий добуток. Його модуль дорiвнює об’єму паралелепiпеда (Spat), утвореного цими трьома векторами.

  ->  ⎧ 2 ⎫     ->  ⎧ 2 ⎫     ->  ⎧ 3 ⎫   
  a = ⎪ 3 ⎪     b = ⎪-1 ⎪     c = ⎪ 9 ⎪
      ⎩ 5 ⎭         ⎩ 7 ⎭         ⎩ 2 ⎭

    ->  ->    ->  
  ( a x b ) · c = 26

Інверсія матриць

Програма обчислює для квадратної матриці порядку n детермінант, ранг та обернену матрицю.

Матриця: 

  ⎧  0  1  1  ⎫
  ⎪  0  1  3  ⎪
  ⎩  2  0  1  ⎭

Обернена матриця

  ⎧  0,25 -0,25  0,5  ⎫
  ⎪   1,5  -0,5    0  ⎪
  ⎩  -0,5   0,5    0  ⎭

Порядок = 3,  Ранг = 3,  Детермінант = 4

Псевдообернена матриця

Якщо стовпці матриці A лінійно незалежні, то A^T· A є оборотною, і за допомогою наступної формули отримують псевдообернену матрицю:

A⁺ = ( A^T· A )^-1· A^T

При цьому A⁺ є лівою оберненою для A , тобто виконується: A⁺ · A = E .

Матриця A
¯¯¯¯¯¯¯¯
  ⎧  1  1  1  1  ⎫
  ⎩  5  7  7  9  ⎭

A^T· A
¯¯¯¯¯
  ⎧  26  36  36  46  ⎫
  ⎪  36  50  50  64  ⎪
  ⎪  36  50  50  64  ⎪
  ⎩  46  64  64  82  ⎭

A^T· A не оборотна

A · A^T
¯¯¯¯¯¯
  ⎧   4   28  ⎫
  ⎩  28  204  ⎭

( A · A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯
  ⎧  6,375 -0,875  ⎫
  ⎩ -0,875  0,125  ⎭

Права обернена:  A^T · ( A · A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧     2  -0,25  ⎫
  ⎪  0,25      0  ⎪
  ⎪  0,25      0  ⎪
  ⎩  -1,5   0,25  ⎭

Множення матриць

Програма обчислює для двох матриць їхню добуткову матрицю.

 1-ша матриця           2-га матриця

  ⎧  1  2  3  0  ⎫   ⎧  1   2   3   4  ⎫
  ⎪  4  5  6  0  ⎪   ⎪  5   6   7   8  ⎪
  ⎪  0  0  0  0  ⎪   ⎪  9  10  11  12  ⎪
  ⎩  0  0  0  0  ⎭   ⎩  0   0   0   0  ⎭

 Добуткова матриця
  
  ⎧  38  44   50   56  ⎫
  ⎪  83  98  113  128  ⎪
  ⎪   0   0   0    0   ⎪
  ⎩   0   0   0    0   ⎭

MatheAss 10.0 − Лiнiйна алгебра

A+ = ( AT· A )-1· AT

A⁺ = ( A^T· A )^-1· A^T