MatheAss 10.0 − 3-вимiрна Геометрiя
Координатнi системи
За допомогою цiєї програми можна перетворювати тривимiрнi декартовi координати у сферичнi або цилiндричнi координати i навпаки.
декартова сферична цилiндрична x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1
Платонiчнi тiла
Програма обчислює п’ять платонiчних тiл: тетраедр, гексаедр, октаедр, додекаедр та iкосаедр, якщо задано довжину ребра, висоту грані, висоту тiла, радiус вписаної кулi, радiус описаної кулi, об’єм або поверхню.
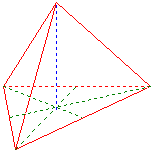
Тетраедр
Дано:
¯¯¯¯¯¯¯¯
Радiус описаної кулi ru = 1
Результати:
¯¯¯¯¯¯¯¯¯¯
Ребро a = 1,6329932
Висота грані h1 = 1,4142136
Висота тiла h2 = 1,3333333
Радiус вписаної кулi ri = 0,33333333
Об’єм V = 0,51320024
Поверхня O = 4,6188022
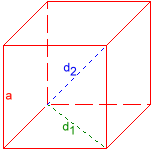
Гексаедр
Дано:
¯¯¯¯¯¯¯¯
Поверхня O = 8
Результати:
¯¯¯¯¯¯¯¯¯¯
Ребро a = 1,1547005
Дiагональ грані d1 = 1,6329932
Просторова дiагональ d2 = 2
Радiус описаної кулi ru = 1
Радiус вписаної кулi ri = 0,57735027
Об’єм V = 1,5396007
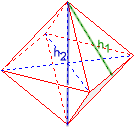
Октаедр
Дано:
¯¯¯¯¯¯¯¯
Об’єм V = 4/3
Результати:
¯¯¯¯¯¯¯¯¯¯
Ребро a = 1,4142136
Висота грані h1 = 1,2247449
Висота тiла h2 = 2
Радiус описаної кулi ru = 1
Радiус вписаної кулi ri = 0,57735027
Поверхня O = 6,9282032
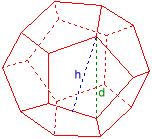
Додекаедр
Дано:
¯¯¯¯¯¯¯¯
Дiагональ грані d = 2
Результати:
¯¯¯¯¯¯¯¯¯
Ребро a = 1,236068
Висота грані h = 1,902113
Радiус описаної кулi ru = 1,7320508
Радiус вписаної кулi ri = 1,3763819
Об’єм V = 14,472136
Поверхня O = 31,543867
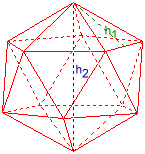
Iкосаедр
Дано:
¯¯¯¯¯¯¯¯
Висота тiла h2 = 2
Результати:
¯¯¯¯¯¯¯¯¯
Ребро a = 1,0514622
Висота грані h1 = 0,910593
Радiус описаної кулi ru = 1
Радiус вписаної кулi ri = 0,79465447
Об’єм V = 2,5361507
Поверхня O = 9,5745414
Iншi тiла
Програма обчислює всi величини правильного призми, прямого кругового цилiндра, квадратної пiрамiди, прямого кругового конуса або кулi, якщо задано двi з них.
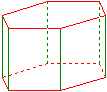
Призма
Дано: n = 4
¯¯¯¯¯¯¯¯
Об’єм V = 1
Поверхня O = 6
Результати:
¯¯¯¯¯¯¯¯¯
Сторона a = 1
Висота h = 1
Радiус описаного кола ru = 0,70710678
Радiус вписаного кола ri = 0,5
Основна площа G = 1
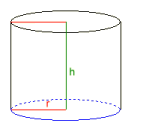
Круговий цилiндр
Дано:
¯¯¯¯¯¯¯¯
Радiус r = 1
Об’єм V = 1
Результати:
¯¯¯¯¯¯¯¯¯¯
Висота h = 0,31830989
Периметр u = 6,2831853
Основна площа G = 3,1415927
Бiчна поверхня M = 2
Поверхня O = 8,2831853
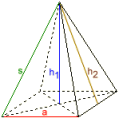
Квадратна пiрамiда
Дано:
¯¯¯¯¯¯¯¯
Основне ребро a = 1
Об’єм V = 1
Результати:
¯¯¯¯¯¯¯¯¯
Бiчне ребро s = 3,082207
Просторова висота h1 = 3
Бiчна висота h2 = 3,0413813
Поверхня O = 7,0827625
Бiчна площа A = 1,5206906
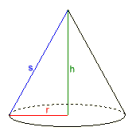
Круговий конус
Дано:
¯¯¯¯¯¯¯¯
Об’єм V = 1
Основна площа G = 1
Результати:
¯¯¯¯¯¯¯¯¯¯
Радiус r = 0,56418958
Висота h = 3
Бiчна лiнiя s = 3,0525907
Бiчна поверхня M = 5,4105761
Поверхня O = 6,4105761
Куля
Дано:
¯¯¯¯¯¯¯¯
Поверхня O = 1
Результати:
¯¯¯¯¯¯¯¯¯¯
Радiус r = 0,28209479
Дiаметр d = 0,56418958
Периметр u = 1,7724539
Об’єм V = 0,094031597
Пряма через 2 точки
Пряма A(1|1|1), B(2|5|6)
Параметричне представлення
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫
x = ⎪ 1 ⎪ + t·⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 5 ⎭
Вiдстань вiд початку координат
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 0,78679579
Положення щодо площини xy
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Перпендикулярна проекцiя:
4·x - y = 3
Точка перетину: S1(0,8|0,2|0)
Кут перетину: 50,490288°
Положення щодо площини yz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Перпендикулярна проекцiя:
5·x - 4·y = 1
Точка перетину: S2(0|-3|-4)
Кут перетину: 8,8763951°
Положення щодо площини xz
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Перпендикулярна проекцiя:
5·x - y = 4
Точка перетину: S3(0,75|0|-0,25)
Кут перетину: 38,112927°
Площина через 3 точки
Площина через точки:
A(1|2|3), B(2|3|3), C(1|0|1)
Точково-напрямна форма:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
Координатне рiвняння:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Вiдстань вiд початку координат:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Точки перетину з осями:
¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)
Куля через 4 точки
Куля через точки:
A(1|0|0), B(0|2|0),
C(0|0|3), D(1|0|1)
Нормальна форма:
¯¯¯¯¯¯¯¯¯¯¯
| -> ⎧-2,5 ⎫ |2
K: | x - ⎪-0,5 ⎪ | = 12,75
| ⎩ 0,5 ⎭ |
Центр i радiус:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-2,5|-0,5|0,5)
r = 3,5707142
Перетини у просторi
Програма обчислює перетини прямих, площин i куль.
двi прямi
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
-> ⎧ 0 ⎫ ⎧ 1 ⎫
h : x = ⎪ 5 ⎪ + s·⎪ 0 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
Точка перетину : S(5|5|5)
Кут перетину: 60°
Вiдстанi до початку координат :
d(O,g)=5 d(O,h)=5
Площина i пряма
-> ⎧ 5 ⎫ ⎧ 0 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
E : x + y + z = 5
Точка перетину : S(5|0|0)
Кут перетину: 54,73561°
Куля i пряма
-> ⎧ 1 ⎫ ⎧ 1 ⎫
g : x = ⎪ 0 ⎪ + r·⎪ 1 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
K : M(5|5|5) , r = 5
Точки перетину :
S1(2,8187|1,8187|1,8187)
S2(8,5147|7,5147|7,5147)
Довжина хорди :
s = 9,8657657
двi площини
Заданi площини:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
E1 : 5·x - 2·y = 5
E2 : 2·x - y + 5·z = 8
Пряма перетину площин:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> |-11 | | 10 |
g : x = |-30 | + r·| 25 |
| 0 | | 1 |
Вiдстань вiд початку координат:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,5057283
Кут перетину площин:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
α = 65,993637°
Двi кулi
Заданi кулi: ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ K1 : M1(3|3|3) , r1 = 3 K2 : M2(1|1|1) , r2 = 3 Коло перетину: ¯¯¯¯¯¯¯¯¯¯¯¯¯ M(2|2|2), r = 2,4494897 Площина перетину: ¯¯¯¯¯¯¯¯¯¯¯¯¯ E : x + y + z = 6
Куля i площина
Площина :
¯¯¯¯¯¯¯
E : 5·x - 4·y + 5·z = -3
Куля :
¯¯¯¯¯¯¯
| -> ⎧ 1 ⎫|2
K : | x - ⎪ 2 ⎪| = 16
| ⎩ 3 ⎭|
Коло перетину K та E :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
M(-0,13636|2,9091|1,8636)
r = 3,548367
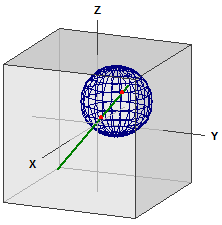
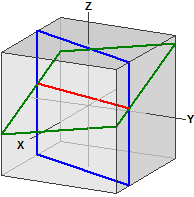
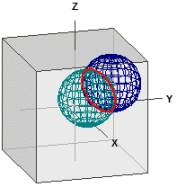
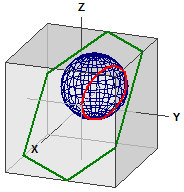
Вiдстанi на кулi
(Нове у версiї 9.0 з грудня 2021)
Обчислюється вiдстань мiж двома точками на кулi. При цьому використовується низка функцiй MatheAss.
GPS десятковi ¯¯¯¯¯¯¯¯¯¯¯ Берлiн : 52.523403, 13.4114 Нью-Йорк : 40.714268, -74.005974 GPS градуси-хвилини-секунди ¯¯¯¯¯¯¯ Берлiн : 52° 31' 24.2508" N, 13° 24' 41.0400" E Нью-Йорк : 40° 42' 51.3648" N, 74° 0' 21.5064" W . . . Вiдстань ¯¯¯¯¯¯¯¯¯¯ d = r · α [рад] = 6385,112
