MatheAss 10.0 − Аналiз
Послiдовностi та ряди (Нове у версiї 9.0 з травня 2021)
Програма визначає перші n членiв послiдовностi (ai) та вiдповiдного ряду (суму членiв послiдовностi), якщо заданi перші члени послiдовностi та явна функцiя ai=ƒ(i) або рекурсивна формула ai=ƒ(a0, a1, ... , ai-1) .
a[0]=1; a[1]=1; a[ i ] = a[i-1] + a[i-2]; n = 20 Послiдовнiсть ¯¯¯¯¯ ( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Ряд ¯¯¯¯¯ ( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
Дiлення полiномiв
Програма обчислює добуток та частку двох полiномiв.
1-й полiном: 3·x4 - 2·x + 1
2-й полiном: 2·x + 5
Добуток: 6·x5 + 15·x4 - 4·x2 - 8·x + 5
Частка: 3/2·x3 - 15/4·x2 + 75/8·x - 391/16
Залишок: 1971/16
Факторизацiя полiномiв (Нове у версiї 9.0)
Програма обчислює рацiональнi нулi та лiнiйну факторизацiю полiнома.
p(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 + x - 9
= (1/9)·(9·x5 - 81·x4 - 82·x3 + 738·x2 + 9·x - 81)
= (1/9)·(3·x - 1)·(3·x + 1)·(x - 9)·(x - 3)·(x + 3)
Рацiональнi нулi: 1/3, -1/3, 9, 3, -3
Перетворення полiномiв (Нове у версiї 9.0)
Полiномiчна функцiя ƒ(x) може бути змiщена або розтягнута у напрямку x та y.
ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Зсув на dx = -2 , dy = 0 ƒ(x + 2) = - 1/4·x4 + 6·x2 + 1
НСД та НСК полiномiв (Нове у версiї 9.0 з лютого 2021)
Програма обчислює найбiльший спiльний дiльник (НСД) та найменше спiльне кратне (НСК) двох полiномiв p1(x) та p2(x).
p1(x) = 4·x6 - 2·x5 - 6·x4- 18·x3 - 2·x2 + 24·x + 8 p2(x) = 10·x4- 14·x3 - 22·x2 + 14·x + 12 НСД(p1,p2) = x2 - x - 2 НСК(p1,p2) = 40·x8 - 36·x7 - 76·x6 - 144·x5 + 88·x4+ 356·x3 - 4·x2 - 176·x - 48
Побудова графiкiв функцiй 1
Можна одночасно побудувати до десяти функцiй в одному координатному системi. Дозволяються також комбiнацiї або похiднi вже визначених функцiй.
Нехай ƒ1(x)=sin(x) та ƒ2(x)=3*sqrt(x), тодi ƒ3(x)=2*y1^2-y2 ƒ3(x)=2*sin(x)^2-3*sqrt(x) ƒ4(x)=f2(y1) ƒ4(x)=3*sqrt(sin(x)) ƒ5(x)=y2' ƒ5(x)=3/(2*sqrt(x))
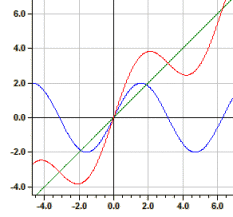
Приклад: ƒ1(x)=sin(x), ƒ2(x)=x та ƒ3(x)=y1+y2
Побудова графiкiв функцiй 2
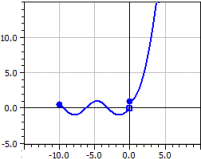
Будується частинами визначена функцiя, яка задається дев’ятьма пiдфункцiями. Для кожної пiдфункцiї вводяться область визначення, тип iнтервалу та колiр. Крiм того, можна визначити, чи малювати граничнi точки чи нi.
Приклад:
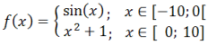
Параметричнi кривi
За допомогою цiєї програми можна малювати кривi, якi не заданi явним функцiональним виразом, а двома функцiями для горизонтального та вертикального вiдхилення.
Приклад: Фiгури Лiссажу
x(k) = sin(3*k)
y(k) = cos(5*k)
k вiд -Pi до Pi
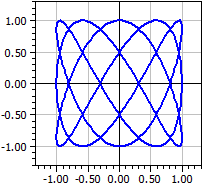
Фiгури Лiссажу отримують, якщо на осцилограф подати двi змiннi напруги рiзної частоти.
Пучки кривих
Програма малює графiки довiльних функцiй, що мiстять параметр k. Значення для k можна перелiчити або визначити через початкове значення, кiнцеве значення та крок.
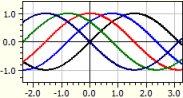
ƒ(x,k) = sin(x+k)
k вiд -2 до 2 з кроком Pi/4
Полiномнi функцiї (Нове у версiї 9.0)
Програма виконує дослiдження кривої для цiлорацiональної функцiї (полiномної функцiї). Тобто визначаються похiднi та первiсна функцiя, функцiя дослiджується на рацiональнi нулi, екстремуми, точки перегину та симетрiю.
Функцiя :
¯¯¯¯¯¯¯¯
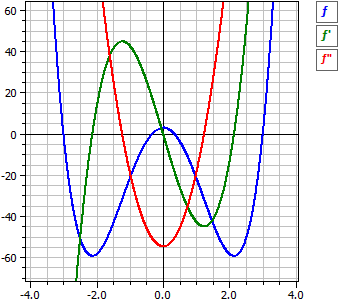
ƒ(x) = 3·x4 - 82/3·x2 + 3
= 1/3·(9·x4 - 82·x2 + 9)
= 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)
Похiднi :
¯¯¯¯¯¯¯¯¯¯
ƒ'(x) = 12·x3 - 164/3·x
ƒ"(x) = 36·x2 - 164/3
ƒ'"(x) = 72·x
Первiсна функцiя
¯¯¯¯¯¯¯¯¯¯¯¯
ƒ(x) = 3/5·x5 - 82/9·x3 + 3·x + c
.
.
.
Раціональні функції (Нове у версії 9.0)
Програма виконує дослідження кривої для (дробово)раціональної функції. Тобто визначаються похідні, розриви визначення та неперервне продовження. Функція досліджується на нулі, екстремуми, точки перегину та поведінку при |x|→∞.
Функція :
¯¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Розриви визначення
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x = 2 полюс зі зміною знаку
x =-2 полюс зі зміною знаку
Похідні :
¯¯¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = —————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ————————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
.
.
.
Дослідження кривої
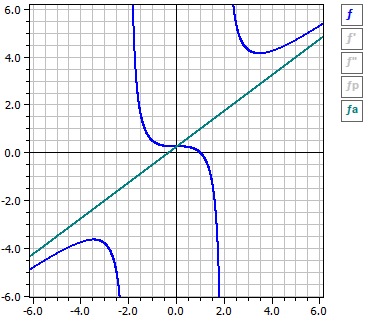
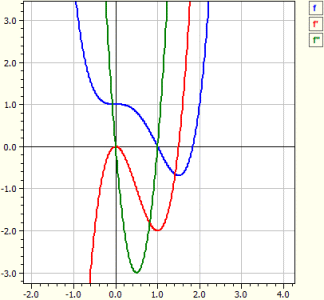
Програма виконує дослідження кривої для довільної функції. Тобто визначаються похідні, функція досліджується на нулі, екстремуми та точки перегину, будуються графіки ƒ, ƒ' та ƒ", а також виводиться таблиця значень.
Функція : ‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ(x) = x^4 - 2*x^3 + 1 Дослідження в області від -10 до 10 Похідні: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ'(x) = 4*x^3-6*x^2 ƒ"(x) = 12*x^2-12*x Нулі: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾ N1( 1 | 0 ) m = -2 N2( 1,83929 | 0 ) m = 4,5912 Екстремуми: ‾‾‾‾‾‾‾‾‾‾‾‾ T1( 1,5 |-0,6875 ) m = 0 Точки перегину: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ W1( 0 | 1 ) m = 0 W2( 1 | 0 ) m =-2
Ітерація Ньютона
Ітерація Ньютона — це наближений метод для обчислення нуля функції ƒ(x). Якщо задати початкове значення x0, яке достатньо близьке до шуканого нуля, то наступне наближення визначається як точка перетину дотичної до графіка ƒ у точці
ƒ(x) = x-cos(x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
Інтегральне числення
(з лютого 2021 з довжинами дуг)
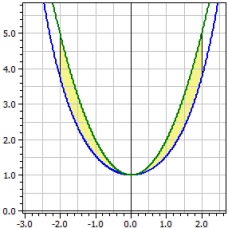
Обчислюється орієнтований та абсолютний вміст площі між
двома графіками функцій на заданому інтервалі. Крім того визначаються:
- моменти при обертанні навколо осі x та y,
- відповідні об’єми тіл обертання,
- довжини дуг на інтервалі [a;b] та
- центр ваги площі (якщо A1=A2).
ƒ1(x) = cosh(x) ƒ2(x) = x^2+1 Інтеграційний інтервал [a;b] від -2 до 2 Орієнтований вміст : A1 = -2,07961 Абсолютний вміст : A2 = 2,07961 Довжини дуг : L1[a;b] = 7,254 L2[a,b] = 9,294
Розклад ряду
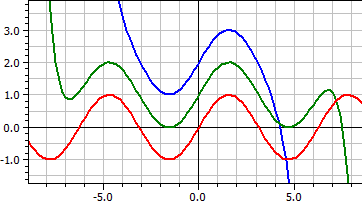
Будується функція, задана у вигляді ряду, причому розклади ряду для різних параметричних областей порівнюються та для кращого розрізнення зміщуються у напрямку y.
Перші 16 членів ряду Тейлора для функції синуса. ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) , k = 4, 8 та 16
Площинні функції
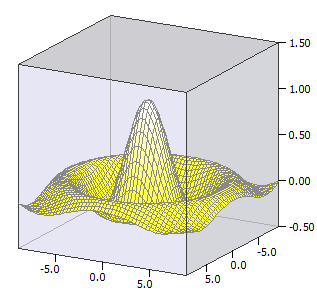
Будується площинна функція ƒ(x,y), тобто тривимірне зображення функції з двома змінними.
Приклад:
ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)
-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5
